题目内容
函数 的定义域为D,若对任意的
的定义域为D,若对任意的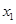 、
、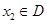 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在D上为“非减函数”.设函数
在D上为“非减函数”.设函数 在
在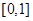 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2) ;(3)
;(3) ,则
,则 、
、 .
.
1、
解析试题分析:根据题意,由于函数 的定义域为D,若对任意的
的定义域为D,若对任意的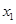 、
、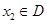 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在D上为“非减函数”.设函数
在D上为“非减函数”.设函数 在
在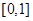 上为“非减函数”,且满足以下三个条件(1)
上为“非减函数”,且满足以下三个条件(1) ;(2)
;(2) ;(3)
;(3) ,那么可知g(1)=1-g(0)=1,
,那么可知g(1)=1-g(0)=1, , 因为当
, 因为当 时,都有
时,都有 ,那么说明了函数为常函数,故
,那么说明了函数为常函数,故
 ,故答案为1、
,故答案为1、
考点:抽象函数及其应用
点评:本题考查的知识点是抽象函数及其应用,其中根据已知中,函数满足的条件,是解答本题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ex(sinx+cosx)在x∈
ex(sinx+cosx)在x∈ 上的值域为 _____________
上的值域为 _____________ ,对任意
,对任意 ,都有
,都有 ,则函数
,则函数 的最大值与最小值之和是 .
的最大值与最小值之和是 . 在R上有两个零点,则实数
在R上有两个零点,则实数 的取值范围是________.
的取值范围是________. 的单调增区间是 .
的单调增区间是 . 上的奇函数
上的奇函数 在
在 上单调递增,且
上单调递增,且 ,则不等式
,则不等式 的解集为______________________.
的解集为______________________. 的定义域为
的定义域为 ,当
,当 时,
时, ,
, ,等式
,等式
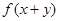 成立,若数列
成立,若数列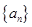 满足
满足 ,且
,且 ,则
,则 的值为
的值为  有实数解,则实数b的范围是_______________
有实数解,则实数b的范围是_______________ 是定义在
是定义在 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
, ,则函数
,则函数 上的解析式是
上的解析式是