题目内容
若函数
在R上有两个零点，则实数
的取值范围是________．
a>2-2ln2
解析试题分析：画出函数f（x）=ex-2x-a的简图，欲使函数f（x）=ex-2x-a在R上有两个零点，由图可知，其极小值要小于0．由此求得实数a的取值范围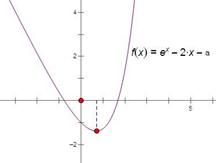
解：令f，（x）=ex-2=0，则x=ln2，∴x＞ln2，f，（x）=ex-2＞0； x＜ln2，f，（x）=ex-2＜0；∴函数f（x）在（ln2，+∞）上是增函数，在（-∞，ln2）上是减函数．∵函数f（x）=ex-2x-a在R上有两个零点，所以f（ln2）=2-2ln2-a＜0，故a＞2-2ln2．故填：（2-2ln2，+∞）．
考点：函数的零点
点评：本题主要考查函数的零点以及数形结合方法，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷
练习册系列答案
相关题目
的零点在区间
上,则
的值为 .
在R是奇函数，且当
时，
，则
时，
的解析式为____ ___________
有两个不同的零点，则实数
的取值范围是 ．
时，函数
在
上有且只有一个零点，则
= 
米，
米. 为了合理利用这块钢板,将在五边形
内截取一个矩形块
，使点
在边
上. 则矩形
面积的最大值为____ 平方米 . 
的定义域为D，若对任意的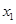
、
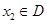，当
时，都有
，则称函数
在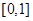
上为“非减函数”，且满足以下三个条件：（1）
；（2）
；（3）
,则
、
．
对任意
都有
，且当
时，
,则
．
在区间[0,1]上是减函数，则实数
的取值范围是 .