题目内容
已知函数 ,对任意
,对任意 ,都有
,都有 ,则函数
,则函数 的最大值与最小值之和是 .
的最大值与最小值之和是 .
3
解析试题分析:因为, ,所以有:设x∈R,t>0,x+t>x,则
,所以有:设x∈R,t>0,x+t>x,则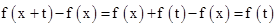
∴f(x)在R上是单调函数,g(x) 在R上是单调函数。
令x=y=0,则f(0)+f(0)=f(0+0)+m,∴f(0)=m
令x=0,y=1,则,f(1)=f(0)+f(1)+m,所以,f(0)=-m,故,m=0.
∴g(x)min +g(x)max =f(-1)+m+ +f(1)+m+
+f(1)+m+ ,2m+
,2m+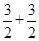 =3.
=3.
考点:函数的单调性,函数的最值.
点评:中档题,利用抽象函数,研究函数的单调性,从而认识到函数取到最值的情况。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
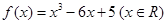 ,若关于
,若关于 的方程
的方程 有三个不同实根,则
有三个不同实根,则 的取值范围是
的取值范围是 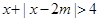 恒成立,则实数
恒成立,则实数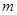 的取值范围是:_ .
的取值范围是:_ . 在R是奇函数,且当
在R是奇函数,且当 时,
时, ,则
,则 时,
时, 的解析式为____ ___________
的解析式为____ ___________ 的定义域为 .
的定义域为 .  有两个不同的零点,则实数
有两个不同的零点,则实数 的取值范围是 .
的取值范围是 . 时,函数
时,函数 在
在 上有且只有一个零点,则
上有且只有一个零点,则 =
=  的定义域为D,若对任意的
的定义域为D,若对任意的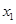 、
、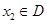 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在
在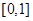 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2) ;(3)
;(3) ,则
,则 、
、 .
. ,函数
,函数 若函数
若函数 在
在 上的最大值比最小值大
上的最大值比最小值大 ,则
,则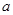 的值为 .
的值为 .