Question

【题目】已知点M，N，P，Q在同一个球面上，且，则该球的表面积是，则四面体MNPQ体积的最大值为（ ）

A.10B.C.12D.5

Answer 1

【答案】A

【解析】

由已知可得△PNM为直角三角形,画出图形,可知要使四面体MNPQ体积取最大值,则球心O在过PM中点O′与面MNP垂直的直线上,由球的表面积求得半径,利用勾股定理求出三棱锥的高,可得四面体MNPQ体积的最大值.

如图,

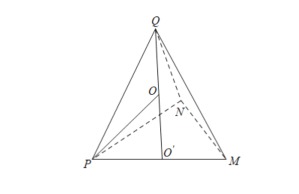
由MN=3,NP=4,MP=5,

可知，所以∠PNM=90°

设四面体MNPQ的外接球的半径为R,由球的表面积是,

得,即R.

要使四面体MNPQ体积取最大值,

则球心O在过PM中点O′与面MNP垂直的直线上,

设QO′=h.

在Rt△OO′P中,OP2=OO′2+O′P2,

∴R2=(h﹣R)2,即,得h=5,

∴四面体MNPQ体积的最大值为.

故选：A.