题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,证明:
,证明:![]() ,当
,当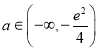 时,函数
时,函数![]() 恒有两个不同零点.
恒有两个不同零点.
【答案】(1)![]() 时,在
时,在![]() 上单调递增;
上单调递增;![]() 时,在
时,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析
上单调递减;(2)证明见解析
【解析】
(1)分别在![]() 和
和![]() 两种情况下讨论导函数的正负,从而得到原函数的单调性;
两种情况下讨论导函数的正负,从而得到原函数的单调性;
(2)将问题转化为当 时,
时,![]() 与
与![]() 恒有两个不同的交点的证明;利用导数可求得
恒有两个不同的交点的证明;利用导数可求得![]() 的单调性和最值,从而确定
的单调性和最值,从而确定![]() 的范围,解得
的范围,解得![]() 的范围.
的范围.
(1)由题意得:![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
综上所述:当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由题意得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,则问题等价于当
,则问题等价于当 时,
时,![]() 与
与![]() 恒有两个不同的交点,
恒有两个不同的交点,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() ,又
,又![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() 与
与![]() 恒有两个不同的交点,
恒有两个不同的交点,
即 ,
,![]() 与
与![]() 恒有两个不同的交点,
恒有两个不同的交点,
![]() 当
当 时,
时,![]() 在
在![]() 上恒有两个不同的零点.
上恒有两个不同的零点.

【题目】滕州市公交公司一切为了市民着想,为方便市区学生的上下学,专门开通了学生公交专线,在学生上学、放学的时间段运行,为了更好地掌握发车间隔时间,公司工作人员对滕州二中车站发车间隔时间与侯车人数之间的关系进行了调查研究,现得到如下数据:
间隔时间 | 10 | 11 | 13 | 12 | 15 | 14 |
侯车人数 | 23 | 25 | 29 | 26 | 31 | 28 |
调查小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据不相邻的概率;
(2)若选取的是前两组数据,请根据后四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的差均不超过1人,则称为最佳回归方程,在(2)中求出的回归方程是否是最佳回归方程?若规定一辆公交车的载客人数不超过35人,则间隔时间设置为18分钟,是否合适?
参考公式: ,
,![]() .
.


