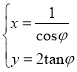题目内容
【题目】如图,![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
(1)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,试判断直线
,试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)设(1)中的直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() ,且点
,且点![]() 满足
满足![]() .记直线
.记直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析;
【解析】
(1)直线![]()
![]() 平面PAC. 连接EF,利用三角形的中位线定理可得,EF
平面PAC. 连接EF,利用三角形的中位线定理可得,EF![]() AC,再利用线面平行的判定定理即可得到
AC,再利用线面平行的判定定理即可得到![]()
![]() 平面ABC,再由线面平行的性质定理可得EF
平面ABC,再由线面平行的性质定理可得EF![]()
![]() ,再利用线面平行的判定定理即可证明直线
,再利用线面平行的判定定理即可证明直线![]()
![]() 平面PAC;
平面PAC;
(2)以![]() 点为原点,向量
点为原点,向量![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系,利用平面的法向量和直线的方向向量可得出线面角,两个直线的方向向量可得出线线角,两个平面的法向量的夹角即可得出二面角,从面即可证明结论.
轴,建立空间直角坐标系,利用平面的法向量和直线的方向向量可得出线面角,两个直线的方向向量可得出线线角,两个平面的法向量的夹角即可得出二面角,从面即可证明结论.
(1)直线![]()
![]() 平面
平面![]() ,证明如下:
,证明如下:
连接EF,因为![]() 分别是
分别是![]() 的中点,所以EF
的中点,所以EF![]() AC,
AC,
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]()
![]() ,
,
所以EF![]()
![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]()
![]() 平面
平面![]()
(2) 由题意得:![]() ,作
,作![]() ,且
,且![]() ,
,
连接![]() ,由(1)可知交线
,由(1)可知交线![]() 即为直线
即为直线![]() ,
,
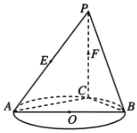
以![]() 点为原点,向量
点为原点,向量![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系( 如图):
轴,建立空间直角坐标系( 如图):
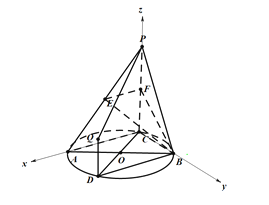
设![]() ,则有
,则有
![]()
所以:![]() ,
,
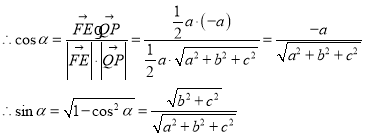
又取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
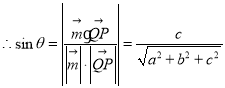 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以由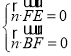 可得
可得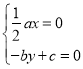 ,令
,令![]() ,
,
则![]() ,
,
 ,
,
![]() ,
,
故 ,
,
即![]()

【题目】滕州市公交公司一切为了市民着想,为方便市区学生的上下学,专门开通了学生公交专线,在学生上学、放学的时间段运行,为了更好地掌握发车间隔时间,公司工作人员对滕州二中车站发车间隔时间与侯车人数之间的关系进行了调查研究,现得到如下数据:
间隔时间 | 10 | 11 | 13 | 12 | 15 | 14 |
侯车人数 | 23 | 25 | 29 | 26 | 31 | 28 |
调查小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据不相邻的概率;
(2)若选取的是前两组数据,请根据后四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的差均不超过1人,则称为最佳回归方程,在(2)中求出的回归方程是否是最佳回归方程?若规定一辆公交车的载客人数不超过35人,则间隔时间设置为18分钟,是否合适?
参考公式: ,
,![]() .
.