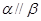题目内容
(本题满分12分)如图,在三棱柱 中,侧面
中,侧面 底面
底面 ,
, ,
, ,且
,且 为
为 中点.
中点.
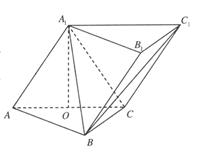
(I)证明: 平面
平面 ;
;
(II)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)在 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点 的位置.
的位置.
 中,侧面
中,侧面 底面
底面 ,
, ,
, ,且
,且 为
为 中点.
中点.
(I)证明:
 平面
平面 ;
;(II)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(III)在
 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点 的位置.
的位置.(I)证明见解析
(II)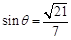
(III) 存在这样的点E,E为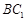 的中点
的中点
(II)
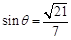
(III) 存在这样的点E,E为
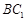 的中点
的中点(1)因为侧面 底面
底面 ,所以只需证明
,所以只需证明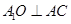 即可.
即可.
(2)可以以O为原点,ON,OC,OA1所在直线为x,y,z轴建立空间直角坐标系,然后用向量的方法求解线面角的问题.
(3)在(2)的基础上也可以用向量来求点E位置.也可以取BC的中点M,连接OM,取BC1的中点E,连接ME,则OM//AB,ME//BB1//AA1,所以平面OMB//平面AA1B,所以OE//平面 .从而确定E为BC1的中点.
.从而确定E为BC1的中点.
(Ⅰ)证明:因为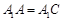 ,且O为AC的中点,
,且O为AC的中点,
所以
又由题意可知,平面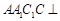 平面
平面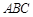 ,交线为
,交线为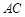 ,且
,且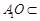 平面
平面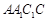 ,
,
所以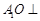 平面
平面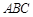
(Ⅱ)如图,以O为原点,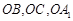 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.

由题意可知,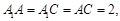 又
又
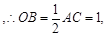
所以得: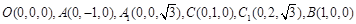
则有: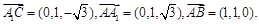
设平面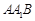 的一个法向量为
的一个法向量为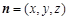 ,则有
,则有
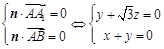 ,令
,令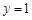 ,得
,得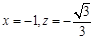
所以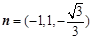
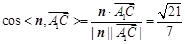
因为直线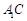 与平面
与平面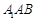 所成角
所成角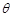 和向量
和向量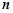 与
与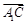 所成锐角互余,所以
所成锐角互余,所以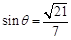
(Ⅲ)设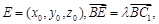
即 ,得
,得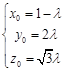
所以 得
得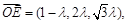
令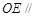 平面
平面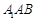 ,得
,得 ,
,
即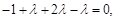 得
得
即存在这样的点E,E为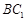 的中点
的中点
 底面
底面 ,所以只需证明
,所以只需证明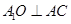 即可.
即可.(2)可以以O为原点,ON,OC,OA1所在直线为x,y,z轴建立空间直角坐标系,然后用向量的方法求解线面角的问题.
(3)在(2)的基础上也可以用向量来求点E位置.也可以取BC的中点M,连接OM,取BC1的中点E,连接ME,则OM//AB,ME//BB1//AA1,所以平面OMB//平面AA1B,所以OE//平面
 .从而确定E为BC1的中点.
.从而确定E为BC1的中点.(Ⅰ)证明:因为
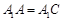 ,且O为AC的中点,
,且O为AC的中点, 所以

又由题意可知,平面
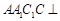 平面
平面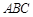 ,交线为
,交线为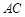 ,且
,且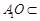 平面
平面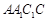 ,
, 所以
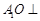 平面
平面
(Ⅱ)如图,以O为原点,
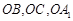 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系. 
由题意可知,
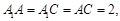 又
又
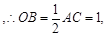
所以得:
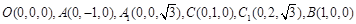
则有:
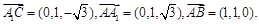
设平面
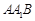 的一个法向量为
的一个法向量为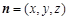 ,则有
,则有 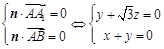 ,令
,令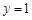 ,得
,得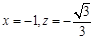
所以
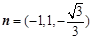
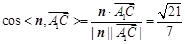
因为直线
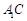 与平面
与平面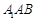 所成角
所成角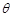 和向量
和向量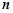 与
与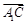 所成锐角互余,所以
所成锐角互余,所以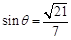
(Ⅲ)设
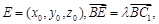
即
 ,得
,得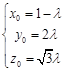
所以
 得
得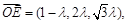
令
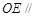 平面
平面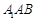 ,得
,得 ,
, 即
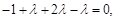 得
得
即存在这样的点E,E为
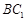 的中点
的中点 
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 中,
中,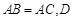 为
为 的中点,
的中点,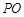 平面
平面 ,垂足
,垂足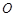 落在线段
落在线段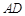 上,已知
上,已知
 ;
;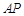 上是否存在点
上是否存在点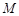 ,使得二面角
,使得二面角 为直二面角?若存在,求出
为直二面角?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 
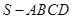 的底面是正方形,
的底面是正方形,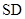 ⊥平面
⊥平面 ,
,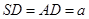 ,点E
,点E .
.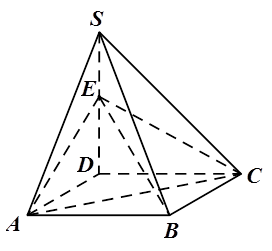
 ,都有AC⊥BE;
,都有AC⊥BE;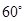 ,求
,求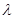 的值.
的值.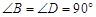 ,
,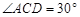 ,
,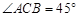 ,
,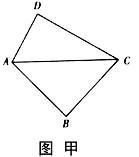
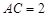 ,现将三角板
,现将三角板 沿
沿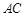 折起,使
折起,使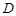 在平面
在平面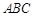 上的射影恰好在
上的射影恰好在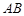 上,如图乙.
上,如图乙.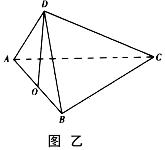
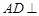 平面
平面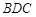 ;
; 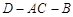 的余弦值;
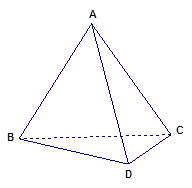
的余弦值;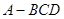 中,面
中,面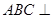 面
面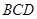 ,
,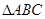 是正三角形,
是正三角形,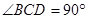 .
.
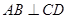 ;
;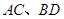 所成角的余弦值为
所成角的余弦值为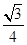 ,求二面角
,求二面角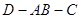 的大小;
的大小;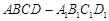 中,
中,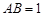 ,
,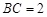 ,
,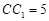 ,
,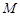 为棱
为棱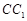 上一点.
上一点.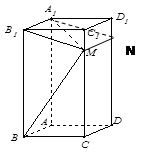
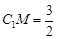 ,求异面直线
,求异面直线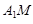 和
和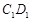 所成角的正切值;
所成角的正切值;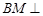 平面
平面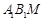 ?若存在,求出
?若存在,求出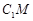 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.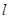 、
、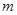 与平面
与平面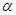 、
、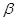 的命题中,正确的是 ( )
的命题中,正确的是 ( )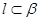 且
且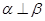 ,则
,则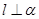 ,
, 且
且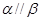 ,则
,则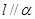 ,
,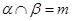 且
且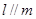 ,则
,则 ,则
,则
 是直二面角,若直线
是直二面角,若直线 则
则
 在平面
在平面 ,则
,则 或
或
 ,则n与
,则n与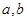 是不同的直线,
是不同的直线,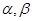 是不同的平面,则下列结论错误的是( )
是不同的平面,则下列结论错误的是( )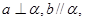 则
则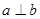
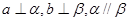 ,则
,则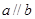
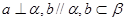 ,则
,则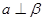
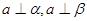 ,则
,则