题目内容
(本题共10分)
将两块三角板按图甲方式拼好,其中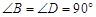 ,
,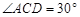 ,
,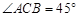 ,
,
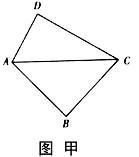
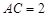 ,现将三角板
,现将三角板 沿
沿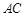 折起,使
折起,使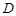 在平面
在平面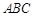 上的射影恰好在
上的射影恰好在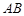 上,如图乙.
上,如图乙.
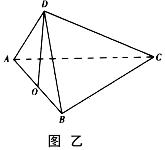
(Ⅰ)求证: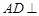 平面
平面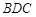 ;
;
(Ⅱ)求二面角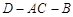 的余弦值;
的余弦值;
将两块三角板按图甲方式拼好,其中
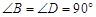 ,
,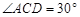 ,
,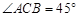 ,
,
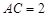 ,现将三角板
,现将三角板 沿
沿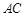 折起,使
折起,使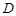 在平面
在平面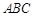 上的射影恰好在
上的射影恰好在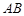 上,如图乙.
上,如图乙.
(Ⅰ)求证:
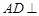 平面
平面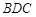 ;
; (Ⅱ)求二面角
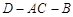 的余弦值;
的余弦值;(Ⅰ)见解析;(Ⅱ) 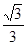
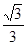
夹角此类问题的关键是熟悉几何体的结构题中,不但利用题中的线面关系夹角平行、垂直、空间角等问题,也可以建立适当的坐标系借助与向量解决以上问题
(1)在平面内找两条相交直线,再分别证明这两条直线与已知直线垂直,即可利用线面垂直的判定定理得到得到线面垂直.
(2)利用题中的垂直关系作出二面角的平面角,再证明此角是所求角,然后放入三角形中利用解三角形的有关知识求解答案即可.
解:(1)设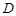 在
在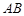 的射影为
的射影为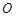 ,则
,则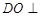 平面
平面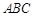 ,
,
 , 又
, 又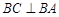 ,
, 平面
平面
 ,又
,又 ,
,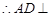 平面
平面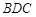 ……………………4分
……………………4分
(2)由(1)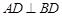 ,又
,又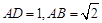 ,
,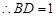
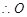 为
为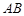 中点
中点
以 为
为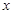 轴,
轴, 为
为 轴,过
轴,过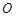 且与
且与 平行的直线为
平行的直线为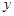 轴建系,则
轴建系,则
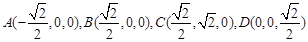
设 为平面
为平面 的法向量,由
的法向量,由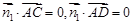 ,可得
,可得
易知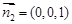 为平面
为平面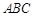 的法向量,
的法向量,
因为所求二面角是锐角,所以所求二面角的余弦值为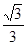 。…………………10分
。…………………10分
(1)在平面内找两条相交直线,再分别证明这两条直线与已知直线垂直,即可利用线面垂直的判定定理得到得到线面垂直.
(2)利用题中的垂直关系作出二面角的平面角,再证明此角是所求角,然后放入三角形中利用解三角形的有关知识求解答案即可.
解:(1)设
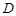 在
在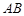 的射影为
的射影为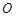 ,则
,则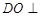 平面
平面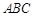 ,
, , 又
, 又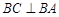 ,
, 平面
平面
 ,又
,又 ,
,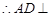 平面
平面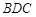 ……………………4分
……………………4分(2)由(1)
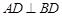 ,又
,又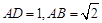 ,
,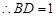
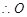 为
为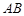 中点
中点以
 为
为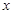 轴,
轴, 为
为 轴,过
轴,过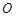 且与
且与 平行的直线为
平行的直线为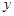 轴建系,则
轴建系,则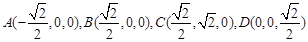
设
 为平面
为平面 的法向量,由
的法向量,由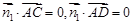 ,可得
,可得
易知
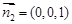 为平面
为平面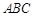 的法向量,
的法向量,
因为所求二面角是锐角,所以所求二面角的余弦值为
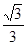 。…………………10分
。…………………10分
练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目

 中,侧面
中,侧面 底面
底面 ,
, ,
, ,且
,且 为
为 中点.
中点.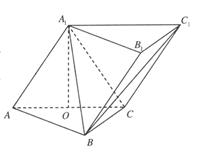
 平面
平面 与平面
与平面 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面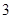 的正三角形
的正三角形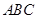 中,
中,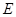 ,
,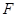 ,
,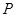 分别为
分别为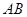 ,
,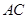 ,
,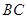 上的点,且满足
上的点,且满足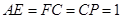 .将△
.将△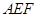 沿
沿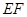 折起到△
折起到△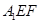 的位置,使二面角
的位置,使二面角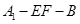 成直二面角,连结
成直二面角,连结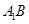 ,
, .(如图2)
.(如图2)
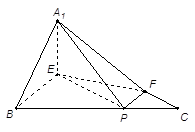
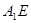 ⊥平面
⊥平面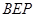 ;
;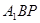 所成角的大小.
所成角的大小.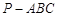 中,
中,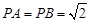 ,
,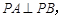
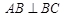 ,
,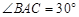 ,平面
,平面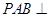 平面
平面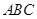 。
。 ;
; 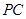 和面
和面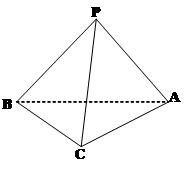
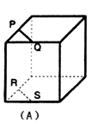
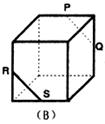
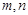 是两条不同的直线,
是两条不同的直线,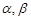 是两个不同的平面,
是两个不同的平面,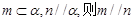 ;
;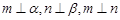 ,则
,则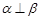 ;
;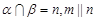 则
则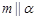 且
且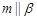 ;
;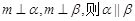
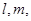 平面
平面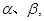 且
且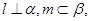 给出下列四个命题:
给出下列四个命题: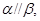 则
则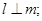 ②若
②若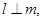 则
则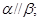
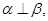 则
则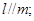 ④若
④若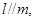 则
则