题目内容
已知函数y=f(x-1)的图象关于直线x=1对称,且当x∈(-∞,0),f(x)+xf′(x)<0成立,若a=(20.2)·f(20.2),b=(ln 2)·f(ln 2),c=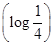 ·f
·f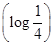 ,则a,b,c的大小关系是( ).
,则a,b,c的大小关系是( ).
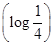 ·f
·f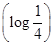 ,则a,b,c的大小关系是( ).
,则a,b,c的大小关系是( ).| A.a>b>c | B.b>a>c |
| C.c>a>b | D.a>c>b |
B
因为函数y=f(x-1)的图象关于直线x=1对称,则y=f(x)关于y轴对称,所以函数y=xf(x)为奇函数.又因为[xf(x)]′=f(x)+xf′(x),所以当x∈(-∞,0)时,[xf(x)]′=f(x)+xf′(x)<0,函数y=xf(x)单调递减;则当x∈(0,+∞)时,函数y=xf(x)单调递减.因为1<20.2<2,0<ln 2<1,log  =2,所以0<ln 2<20.2<log
=2,所以0<ln 2<20.2<log  ,所以b>a>c.
,所以b>a>c.
 =2,所以0<ln 2<20.2<log
=2,所以0<ln 2<20.2<log  ,所以b>a>c.
,所以b>a>c.
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
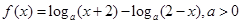 且
且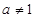 .
.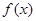 的定义域;
的定义域;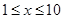 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是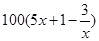 元.
元.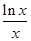
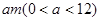 、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为
、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为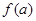 ,若将这棵树围在花圃中,则函数
,若将这棵树围在花圃中,则函数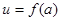 的图象大致是( )
的图象大致是( )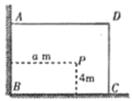
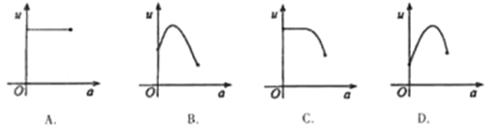
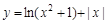 ,满足
,满足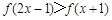 ,则
,则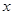 的取值范围是 .
的取值范围是 .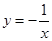 在
在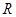 上单调递增;
上单调递增;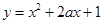 在
在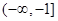 上单调递减,则
上单调递减,则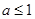 ;
;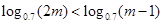 ,则
,则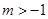 ;
;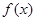 是定义在
是定义在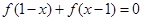 .
.