题目内容
函数 在一点的导数值为
在一点的导数值为 是函数
是函数 在这点取极值的 条件。
在这点取极值的 条件。
 在一点的导数值为
在一点的导数值为 是函数
是函数 在这点取极值的 条件。
在这点取极值的 条件。既不充分也不必要条件
试题分析:对于可导函数
 不能推出
不能推出 在
在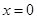 取极值,
取极值,故导数为0时不一定取到极值,而对于任意的函数,当可导函数在某点处取到极值时,此点处的导数不一定存在,更不用说为0了.例如
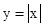 ,在
,在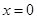 x=0处取极值.,但在
x=0处取极值.,但在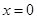 x=0处没有导数.数
x=0处没有导数.数 在一点的导数值为
在一点的导数值为 是函数
是函数 在这点取极值的既不充分也不必要条件
在这点取极值的既不充分也不必要条件
练习册系列答案
相关题目
题目内容
 在一点的导数值为
在一点的导数值为 是函数
是函数 在这点取极值的 条件。
在这点取极值的 条件。 不能推出
不能推出 在
在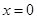 取极值,
取极值,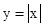 ,在
,在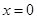 x=0处取极值.,但在
x=0处取极值.,但在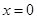 x=0处没有导数.数
x=0处没有导数.数 在一点的导数值为
在一点的导数值为 是函数
是函数 在这点取极值的既不充分也不必要条件
在这点取极值的既不充分也不必要条件