题目内容
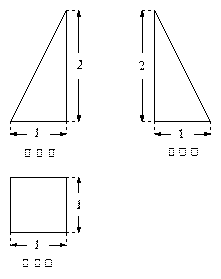
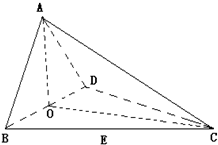
四面体ABCD中,AB=BC==CD=DB,点A在面BCD上的射影恰是CD的中点,则对棱BC与AD所成的角等于( )
A.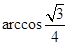 | B.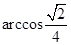 | C.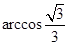 | D.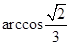 |
B.
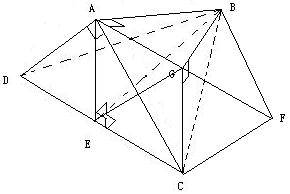
AB=BC=CD=DB.所以△BCD是等边三角形。
△ABD与△ABC△ADC都是等腰三角形
因为E是A的投影,所以AE垂直于△BCD所在平面
因为△ADC经过AE
所以△ADC与△BCD所在的平面是相互垂直的两个平面
这样,由于AE垂直于BE,AB=BC=DB
△ABE与△ADE与△ACE是全等三角形
所以AE=DE=EC,所以△ADC是直角等腰三角形
现在过A做DC的平行线AF,并使DC与AF等长
连接CF,这样CF与AD平行
所以AD与BC所形成的角度和CF与BC所形成的角度相等
连接B、C与AF中点G形成BG、CG
设AE长度为1,则AC=√2, AB=AC=2
因为G为AF中点,AG=GF=1
连接EG
因为BE垂直于EG
BE=√3,EG=√2,所以BG=√5
因为BC^2+CG^2=BG^2,所以在△BGC中∠BGC是直角
又因为AB^2+AG^2=BG^2,所以△ABG是直角三角形△ABF是等边直角三角形
BF=2√2
这样,在△BCF中,BC=2,CF=√2,BF=2√2
所以问题归结为求CF与BC所形成的角度∠C的过程
已知三边求一角的过程
由余弦定理知
BF^2= BC^2+CF^2-2BC*CF*cos∠C
求得角C为
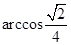

练习册系列答案
相关题目
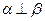 ,
,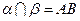 ,
,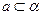 ,
,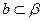 ,若
,若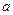 ,
,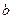 与
与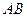 都不垂直.
都不垂直.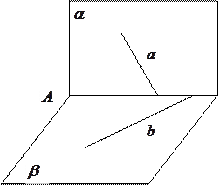
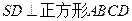 ,
,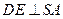 于
于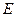 ,
,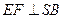 于
于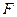 ,
,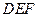 交
交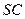 于
于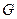 .(1)求证:
.(1)求证: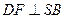 ;(2)求证:
;(2)求证: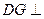 平面
平面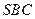 .
.
 a,侧棱AA1=2a,点D是AA1的中点,那么截面DBC与底面ABC所成二面角的大小是________.
a,侧棱AA1=2a,点D是AA1的中点,那么截面DBC与底面ABC所成二面角的大小是________. 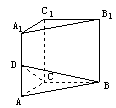
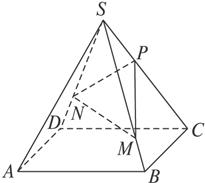
 的棱长都为
的棱长都为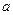 ,底面
,底面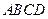 是菱形,且
是菱形,且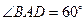 ,侧棱
,侧棱 ,
,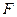 为棱
为棱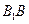 的中点,
的中点,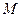 为线段
为线段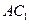 的中点.
的中点.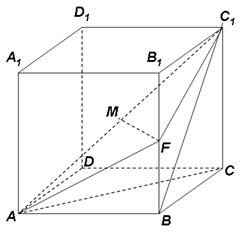
 ;
;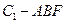 的体积.
的体积.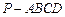 的三视图如图
的三视图如图 所示,则四棱锥
所示,则四棱锥