题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若函数![]() 在
在![]() 处取得极小值,求实数a的取值范围.
处取得极小值,求实数a的取值范围.
【答案】(1)函数![]() 在区间
在区间![]() 单调递减(2)
单调递减(2)![]()
【解析】
(1)当![]() 时,求得函数的导数
时,求得函数的导数![]() ,构造函数
,构造函数![]() ,利用导数求得
,利用导数求得![]() 的单调性与最值,进而得出
的单调性与最值,进而得出![]() 的符号,即可求解函数
的符号,即可求解函数![]() 的单调性;
的单调性;
(2)求得函数![]() 导数
导数![]() ,构造新函数
,构造新函数![]() ,求得
,求得![]() 的导数,分
的导数,分![]() ,
,![]() ,
,![]() ,
,![]() 四种情况讨论,求得
四种情况讨论,求得![]() 的单调性与最值,得出
的单调性与最值,得出![]() 单调性,即可求解
单调性,即可求解![]() 的极值,进而得到
的极值,进而得到![]() 的范围.
的范围.
(1)当![]() 时,
时,![]() ,定义域为
,定义域为![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
![]() 的最大值为
的最大值为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]()
所以函数![]() 在区间
在区间![]() 单调递减
单调递减
(2)由已知得:![]() ,则
,则![]() ,
,
记![]() ,则
,则![]() ,
,![]() ,
,
①若![]() 时,则当
时,则当![]() 时
时![]() ,
,![]() 在
在![]() 单调递增
单调递增
且当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,即
,即![]()
又![]() ,所以函数
,所以函数![]() 在
在![]() 处取得极小值,满足题意.
处取得极小值,满足题意.
②若![]() 时,则
时,则![]() ,当
,当![]() 时,
时,![]() ,故函数
,故函数![]() 区间
区间![]() 单调递增,
单调递增,
且当![]() 时
时![]() 即
即![]()
当![]() 时
时![]() ,即
,即![]()
又![]() ,所以函数
,所以函数![]() 在
在![]() 处取得极小值,满足题意.
处取得极小值,满足题意.
③若![]() 时,则
时,则![]() ,由(1)知函数
,由(1)知函数![]() 在区间
在区间![]() 单调递减,
单调递减,
故![]() 在区间
在区间![]() 单调递减,不满足题意.
单调递减,不满足题意.
④若![]() 时,则
时,则![]() ,当
,当![]() 时
时![]() ,故函数
,故函数![]() 在
在![]() 单调递减
单调递减
且当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,即
,即![]() ,又
,又![]() ,
,
所以函数![]() 在
在![]() 处取得极大值,不满足题意.
处取得极大值,不满足题意.
综上,实数a的取值范围是![]()

【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: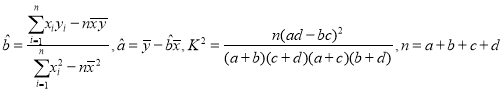 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|


