题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线交
的直线交![]() 轴正半轴于点
轴正半轴于点![]() ,交抛物线于
,交抛物线于![]() 两点,其中点
两点,其中点![]() 在第一象限.
在第一象限.
(Ⅰ)求证:以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切;
轴相切;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)证明见解析; (Ⅱ) ![]() .
.
【解析】
试题(Ⅰ)题意实质上证明线段![]() 的中点到
的中点到![]() 轴的距离等于线段
轴的距离等于线段![]() 长的一半,根据抛物线的定义设
长的一半,根据抛物线的定义设![]() 可证得;(Ⅱ)同样设
可证得;(Ⅱ)同样设![]() ,
,![]() ,把已知
,把已知![]() ,
,![]() 用坐标表示出来,消去坐标
用坐标表示出来,消去坐标![]() 及
及![]() ,得出
,得出![]() 与
与![]() 的关系
的关系![]() ,此时就可得出
,此时就可得出![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由已知![]() ,设
,设![]() ,则
,则![]() ,
,
圆心坐标为![]() ,圆心到
,圆心到![]() 轴的距离为
轴的距离为![]() ,
,
圆的半径为![]() ,
,
所以,以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切.
轴相切.
(Ⅱ)解法一:设![]() ,由
,由![]() ,
,![]() ,得
,得
![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,
,
由![]() ,得
,得![]() .
.
又![]() ,
,![]() ,
,
所以![]() .
.
代入![]() ,得
,得![]() ,
,![]() ,
,
整理得![]() ,
,
代入![]() ,得
,得![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
解法二:设![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
所以![]() (*),
(*),
由![]() ,
,![]() ,得
,得
![]() ,
,![]() ,
,
所以,![]() ,
,
![]() ,
,
将![]() 代入(*)式,得
代入(*)式,得![]() ,
,
所以![]() ,
,![]() .
.
代入![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】为了解重庆市高中学生在面对新高考模式“3+1+2”的科目选择中,物理与历史的二选一是否与性别有关,某高中随机对该校50名高一学生进行了问卷调查得到相关数据如下列联表:
选物理 | 选历史 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
己知在这50人中随机抽取1人,抽到选物理的人的概率为![]() 。
。
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为物理与历史的二选一与性别有关?
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式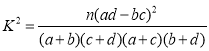 ,其中
,其中![]() 为样本容量)
为样本容量)
(2)己知在选物理的10位女生中有3人选择了化学、地理,有5人选择了化学、生物,有2人选择了生物、地理,现从这10人中抽取3人进行更详细的学科意愿调查,记抽到的3人中选择化学的有X人,求随机变量X的分布列及数学期望。