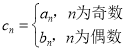题目内容
【题目】已知直线![]() 的参数方程为
的参数方程为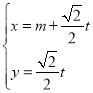 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
【答案】(Ⅰ)曲线![]() 的参数方程为:
的参数方程为: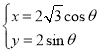 (
(![]() 为参数);
为参数);![]() 的极坐标方程为
的极坐标方程为![]() ;(Ⅱ)16.
;(Ⅱ)16.
【解析】
(I)直接利用转换关系,把参数方程、极坐标方程和直角坐标方程之间进行转换;
(II)利用三角函数关系式的恒等变换和正弦型函数的性质的应用,即可求出结果.
(Ⅰ) 由题意:曲线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
所以曲线![]() 的参数方程为
的参数方程为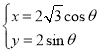 (
(![]() 为参数),
为参数),
因为直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
又因曲线![]() 的左焦点为
的左焦点为![]() ,将其代入
,将其代入![]() 中,得到
中,得到![]() ,
,
所以![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅱ)设椭圆![]() 的内接矩形的顶点为
的内接矩形的顶点为![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
所以椭圆![]() 的内接矩形的周长为:
的内接矩形的周长为:,
所以当![]() 时,即
时,即![]() 时,椭圆
时,椭圆![]() 的内接矩形的周长取得最大值16 .
的内接矩形的周长取得最大值16 .

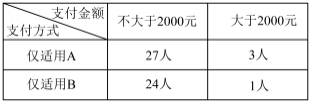
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() 倍B.
倍B.![]() 倍C.
倍C.![]() 倍D.
倍D.![]() 倍
倍
【题目】在世界读书日期间,某地区调查组对居民阅读情况进行了调查,获得了一个容量为200的样本,其中城镇居民140人,农村居民60人.在这些居民中,经常阅读的城镇居民有100人,农村居民有30人.
(1)填写下面列联表,并判断能否有99%的把握认为经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
(2)从该地区城镇居民中,随机抽取5位居民参加一次阅读交流活动,记这5位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的期望.
的期望.
附: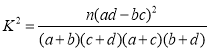 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】BMI指数是用体重公斤数除以身高米数的平方得出的数值,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重,当BMI数值小于20.5时,我们说体重较轻,身高大于或等于170cm时,我们说身高较高,身高小于170cm时,我们说身高较矮.某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
(1)根据最小二乘法的思想与公式求得线性回归方程![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值![]() (保留两位有效数字);
(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重(kg) | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | ﹣1.5 | ﹣0.5 |
(2)通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58(kg).请重新根据最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
参考公式: 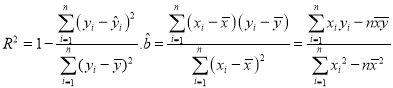 ,
,![]() .
.![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.