ĢāÄæÄŚČŻ
”¾ĢāÄæ”æBMIÖøŹżŹĒÓĆĢåÖŲ¹«½ļŹż³żŅŌÉķøßĆ׏żµÄĘ½·½µĆ³öµÄŹżÖµ£¬ŹĒ¹ś¼ŹÉĻ³£ÓƵÄŗāĮæČĖĢåÅÖŹŻ³Ģ¶ČŅŌ¼°ŹĒ·ń½”æµµÄŅ»øö±ź×¼.¶ŌÓŚøßÖŠÄŠĢåÓżĢŲ³¤Éś¶ųŃŌ£¬µ±BMIŹżÖµ“óÓŚ»ņµČÓŚ20.5Ź±£¬ĪŅĆĒĖµĢåÖŲ½ĻÖŲ£¬µ±BMIŹżÖµŠ”ÓŚ20.5Ź±£¬ĪŅĆĒĖµĢåÖŲ½ĻĒį£¬Éķøß“óÓŚ»ņµČÓŚ170cmŹ±£¬ĪŅĆĒĖµÉķøß½Ļøߣ¬Éķøߊ”ÓŚ170cmŹ±£¬ĪŅĆĒĖµÉķøß½Ļ°«.ij֊Š”ѧɜ³É³¤Óė·¢Õ¹»ś¹¹“ÓijŹŠµÄ320ĆūøßÖŠÄŠĢåÓżĢŲ³¤ÉśÖŠĖ껜єȔ8Ćū£¬ĘäÉķøßŗĶĢåÖŲµÄŹż¾ŻČē±ķĖłŹ¾£ŗ
±ąŗÅ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ÉķøߣØcm£© | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
ĢåÖŲ£Økg£© | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
£Ø1£©øł¾Ż×īŠ”¶ž³Ė·ØµÄĖ¼ĻėÓė¹«Ź½ĒóµĆĻߊŌ»Ų¹é·½³Ģ![]() .ĄūÓĆŅŃ¾ĒóµĆµÄĻߊŌ»Ų¹é·½³Ģ£¬ĒėĶźÉĘĻĀĮŠ²Š²ī±ķ£¬²¢Ēó½āŹĶ±äĮæ£ØÉķøߣ©¶ŌÓŚŌ¤±Ø±äĮæ£ØĢåÖŲ£©±ä»ÆµÄ¹±Ļ×Öµ
.ĄūÓĆŅŃ¾ĒóµĆµÄĻߊŌ»Ų¹é·½³Ģ£¬ĒėĶźÉĘĻĀĮŠ²Š²ī±ķ£¬²¢Ēó½āŹĶ±äĮæ£ØÉķøߣ©¶ŌÓŚŌ¤±Ø±äĮæ£ØĢåÖŲ£©±ä»ÆµÄ¹±Ļ×Öµ![]() £Ø±£ĮōĮ½Ī»ÓŠŠ§Źż×Ö£©£»
£Ø±£ĮōĮ½Ī»ÓŠŠ§Źż×Ö£©£»
±ąŗÅ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ÉķøߣØcm£© | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
ĢåÖŲ£Økg£© | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
²Š²ī | 0.1 | 0.3 | 0.9 | ©1.5 | ©0.5 |
£Ø2£©Ķعż²Š²ī·ÖĪö£¬¶ŌÓŚ²Š²īµÄ×ī“ó£Ø¾ų¶ŌÖµ£©µÄÄĒ×鏿¾Ż£¬ŠčŅŖČ·ČĻŌŚŃł±¾µćµÄ²É¼ÆÖŠŹĒ·ńÓŠČĖĪŖµÄ“ķĪó.ŅŃÖŖĶعżÖŲŠĀ²É¼Æ·¢ĻÖ£¬øĆ×鏿¾ŻµÄĢåÖŲÓ¦øĆĪŖ58£Økg£©.ĒėÖŲŠĀøł¾Ż×īŠ”¶ž³Ė·ØµÄĖ¼ĻėÓė¹«Ź½£¬Ēó³öÄŠĢåÓżĢŲ³¤ÉśµÄÉķøßÓėĢåÖŲµÄĻߊŌ»Ų¹é·½³Ģ.
²Īæ¼¹«Ź½£ŗ 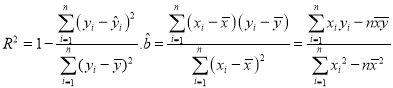 £¬
£¬![]() .
.![]() .
.
²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() .
.
”¾“š°ø”æ£Ø1£©Ģī±ķ¼ū½āĪö;![]() ;£Ø2£©
;£Ø2£©![]() .
.
”¾½āĪö”æ
£Ø1£©ÓɱķÖŠµÄŹż¾ŻæÉĒó³öĻߊŌ»Ų¹é·½³ĢĪŖ![]() £¬½ų¶ųæÉĶźÉĘĖłøų±ķøń£¬Ēó³öĖłÓŠ²Š²īÖµ.ÓÉ
£¬½ų¶ųæÉĶźÉĘĖłøų±ķøń£¬Ēó³öĖłÓŠ²Š²īÖµ.ÓÉ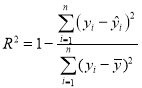 ¼“æÉĒó³ö¹±Ļ×Öµ
¼“æÉĒó³ö¹±Ļ×Öµ![]() .
.
£Ø2£©¼ĘĖ抎¶©ŗó![]() ŅŌ¼°
ŅŌ¼°![]() £¬“śČėµ½
£¬“śČėµ½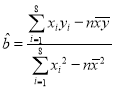 £¬
£¬![]() ½ų¶ųæÉĒó³öĻߊŌ»Ų¹é·½³Ģ.
½ų¶ųæÉĒó³öĻߊŌ»Ų¹é·½³Ģ.
½ā£ŗ£Ø1£©ÓÉĢāŅāÖŖĻߊŌ»Ų¹é·½³ĢĪŖ![]() £¬¼ĘĖć
£¬¼ĘĖć![]() £¬
£¬![]() £¬
£¬![]() .ĶźÉĘĻĀĮŠ²Š²ī±ķČēĻĀ£¬
.ĶźÉĘĻĀĮŠ²Š²ī±ķČēĻĀ£¬
±ąŗÅ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ÉķøߣØcm£©xi | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
ĢåÖŲ£Økg£©yi | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
²Š²ī | 0.1 | 0.3 | 0.9 | ©1.5 | ©0.5 | ©2.3 | ©0.5 | 3.5 |
¼ĘĖć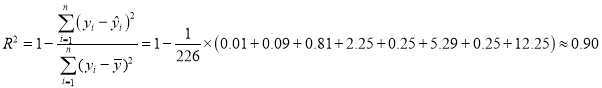 £¬
£¬
ĖłŅŌ½āŹĶ±äĮæ£ØÉķøߣ©¶ŌÓŚŌ¤±Ø±äĮæ£ØĢåÖŲ£©±ä»ÆµÄ¹±Ļ×Öµ![]() .
.
£Ø2£©Ķعż²Š²ī·ÖĪöÖŖ£¬²Š²īµÄ×ī“ó£Ø¾ų¶ŌÖµ£©µÄÄĒ×鏿¾ŻĪŖµŚ8×飬ĒŅ![]()
ÓÉ![]() £¬¼ĘĖ抎¶©ŗó
£¬¼ĘĖ抎¶©ŗó![]()
ÓÖ![]() £¬
£¬![]() £¬ŠŽ¶©ŗó
£¬ŠŽ¶©ŗó![]() .
.
ĖłŅŌ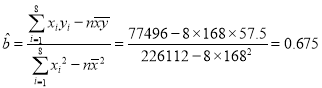 £¬
£¬
![]() .
.
ĖłŅŌ![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄĻߊŌ»Ų¹é·½³ĢŹĒ
µÄĻߊŌ»Ų¹é·½³ĢŹĒ![]() .
.

 ĢŲøß¼¶½ĢŹ¦µć²¦ĻµĮŠ“š°ø
ĢŲøß¼¶½ĢŹ¦µć²¦ĻµĮŠ“š°ø