题目内容
已知
=(x,0),
=(1,y),且(
+
)⊥(
-
).
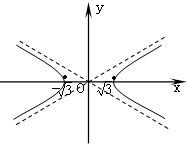
(1)求点P(x,y)的轨迹C的方程,且画出轨迹C的草图;
(2)若直线l:y=kx+m(k≠0)与上述曲线C交于不同的两点A、B,求实数k和m所满足的条件;
(3)在(2)的条件下,若另有定点D(0,-1),使|AD|=|BD|,试求实数m的取值范围.

| a |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
(1)求点P(x,y)的轨迹C的方程,且画出轨迹C的草图;
(2)若直线l:y=kx+m(k≠0)与上述曲线C交于不同的两点A、B,求实数k和m所满足的条件;
(3)在(2)的条件下,若另有定点D(0,-1),使|AD|=|BD|,试求实数m的取值范围.

(1)(
+
)⊥(
-
)⇒(
+
)•(
-
)=0
⇒
2=3
2⇒x2=3(y2+1)
∴P(x,y)的轨迹C的方程为
-y2=1
其草图如右.(注:不画渐近线,不得分)
(2)
⇒(1-3k2)x2-6kmx-3m2-3=0
⇒
(*)
(3)设A(x1,y1)、B(x2,y2),A、B中点为H(x0,y0),
则x0=
=
,y0=kx0+m=
,
由题意,有AB⊥DH⇒kAB•kDH=-1
⇒k•
=-1 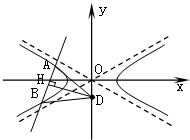
⇒3k2=4m+1,
代入(*),得
⇒-
<m<0或m>4.
| a |
| 3 |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
⇒
| a |
| b |
∴P(x,y)的轨迹C的方程为
| x2 |
| 3 |
其草图如右.(注:不画渐近线,不得分)
(2)
|
|
|
(3)设A(x1,y1)、B(x2,y2),A、B中点为H(x0,y0),
则x0=
| x1+x2 |
| 2 |
| 3km |
| 1-3k2 |
| m |
| 1-3k2 |
由题意,有AB⊥DH⇒kAB•kDH=-1
⇒k•
| ||
|

⇒3k2=4m+1,
代入(*),得
|
⇒-
| 1 |
| 4 |


练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目


 的直径
的直径 ,
, 是
是 延长线上的一点,过
延长线上的一点,过 ,连接
,连接 ,若
,若 ,
,
 .
.
