题目内容
有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)共有多少种放法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒不放球,有多少种放法?
(1)256(2)144(3)144(4)84
解析试题分析:(1)一个球一个球地放到盒子里去,每只球都可有4种独立的放法,由分步乘法计数原理,放法共有: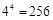 种.
种.
(2)为保证“恰有一个盒子不放球”,先从四个盒子中任意拿出去1个,即将4个球分成2,1,1的三组,有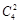 种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法:
种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法: 种.
种.
(3)“恰有一个盒内放2个球”,即另外三个盒子中恰有一个空盒.因此,“恰有一个盒内放2球”与“恰有一个盒子不放球”是一回事.故也有144种放法.
(4)先从四个盒子中任意拿走两个有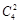 种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有
种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有 种放法;第二类:有
种放法;第二类:有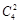 种放法.因此共有
种放法.因此共有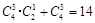 种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有:
种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有: 种.
种.
考点:本小题主要考查两个计数原理和排列组合的综合应用.
点评:两个计数原理是解决这类问题的基础,而排列组合的准确灵活应用是解决这类问题的关键,要分清是排列问题还是组合问题,是分类还是分步,要坚持特殊元素优先和特殊位置优先的原则.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
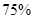 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.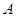 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为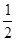 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区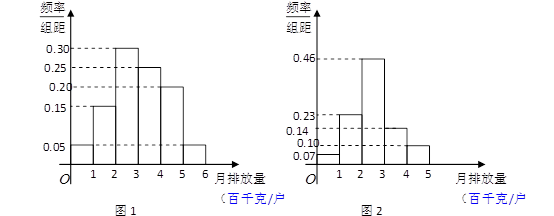
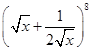 的展开式中,求
的展开式中,求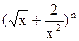 的第五项的二项式系数与第三项的二项式系数比为14:3,求展开式中的常数项.
的第五项的二项式系数与第三项的二项式系数比为14:3,求展开式中的常数项.