题目内容
有6本不同的书,按照以下要求处理,各有多少种不同的分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
(1)
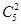
 =60种.
=60种.
(2)
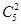
 ="60" 种.
="60" 种.
(3)
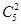

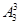 =360(种).
=360(种).
(4)一共有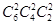 =90种方法.
=90种方法.
(5) (种)。
(种)。
解析试题分析:(1)先在6本书中任取一本.作为一本一堆,有 种取法,再从余下的五本书中任取两本,作为两本一堆,有
种取法,再从余下的五本书中任取两本,作为两本一堆,有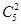 种取法,再后从余下三本取三本作为一堆,有
种取法,再后从余下三本取三本作为一堆,有 种取法,故共有分法
种取法,故共有分法
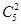
 =60种. 3分
=60种. 3分
(2)由(1)知.分成三堆的方法有
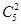
 种,而每种分组方法仅对应一种分配方法,故甲得一本,乙得二本,丙得三本的分法亦为
种,而每种分组方法仅对应一种分配方法,故甲得一本,乙得二本,丙得三本的分法亦为
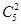
 ="60" 种. 6分
="60" 种. 6分
(3)由(1)知,分成三堆的方法有
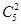
 种,但每一种分组方法又有
种,但每一种分组方法又有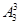 不同的分配方案,故一人得一本,一人得两本,一人得三本的分法有
不同的分配方案,故一人得一本,一人得两本,一人得三本的分法有
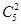

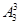 =360(种).
=360(种).
9分
(4)3个人一个一个地来取书,甲从6本不同的书本中任取出2本的方法有 种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有
种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有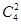 种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有
种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有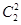 种方法,
种方法,
所以一共有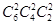 =90种方法. 12分
=90种方法. 12分
(5)把6本不同的书分成三堆,每堆二本与把六本不同的书分给甲、乙、丙三人,每人二本的区别在于,后者相当于把六本不同的书,平均分成三堆后,再把每次分得的三堆书分给甲、乙、丙三个人.因此,设把六本不同的书,平均分成三堆的方法有 种,那么把六本不同的书分给甲、乙、丙三人每人2本的分法就应
种,那么把六本不同的书分给甲、乙、丙三人每人2本的分法就应 种,由(4)知,把六本不同的书分给甲、乙、丙三人,每人2本的方法有
种,由(4)知,把六本不同的书分给甲、乙、丙三人,每人2本的方法有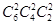 种.
种.
所以 ,则
,则 (种) 15分
(种) 15分
考点:本题主要考查排列组合中的“分组问题”。
点评:典型题,本题涵盖了所有情况下“分组问题”,其解法具有较强的代表性,可作为“经典”理解、掌握。要注意分组中的“均匀不均匀”、“编号不编号”等条件。

如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
| 所用时间(min) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2人数 | 0 | 4 | 16 | 16 | 4 |
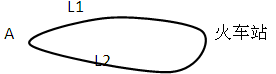
(1)试估计40 min内不能赶到火车站的概率
(2)现甲有40 min时间赶往火车站,为尽最大可能在允许的时间内赶到火车站,试通过计算说明,他如何选路径
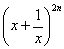 展开式中,第四项与第六项的系数相等。求
展开式中,第四项与第六项的系数相等。求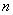 ,并求展开式中的常数项;
,并求展开式中的常数项;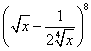 展开式中的所有的有理项。
展开式中的所有的有理项。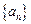 的前
的前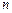 项和为
项和为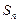 ,
,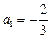 ,满足
,满足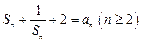
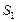 、
、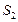 、
、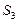 、
、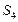 ,并猜想
,并猜想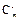 +2
+2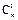 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为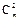 +22
+22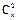 =
=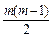 +2n(n-1)=
+2n(n-1)=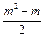 +(11-m)(
+(11-m)(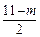 -1)=(m-
-1)=(m-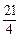 )2+
)2+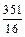 .
. 33,
33,