题目内容
【题目】定义“等和数列”：在一个数列中，如果每一个项与它的后一项的和都为同一个常数，那么这个数列就叫做“等和数列”，这个常数叫做公和．已知数列{an}是等和数列，且a1=2，公和为6，求这个数列的前n项的和S= ．
【答案】
【解析】解：由题意知，an+an+1=6，且a1=2，所以，a1+a2=6，得a2=4，a3=2，a4=4，…a2n﹣1=2，a2n=4…，
当n为偶数时sn=（2+4）+（2+4）+（2+4）+…+（2+4）=6× 
=3n，
当n为奇数时sn=（2+4）+（2+4）+…（2+4）+2=6× 
+2=3n﹣1，
所以答案是： 
．
【考点精析】利用数列的前n项和对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系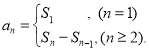
．
练习册系列答案
相关题目
