题目内容
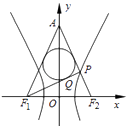
【题目】已知直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4sin(θ﹣
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4sin(θ﹣ ![]() ).
).
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面ρ≤4sin(θ﹣ ![]() )的公共点,求
)的公共点,求 ![]() x+y的取值范围.
x+y的取值范围.
【答案】
(1)解:因为圆C的极坐标方程为ρ=4sin(θ﹣ ![]() ),
),
所以ρ2=4ρ( ![]() sinθ﹣
sinθ﹣ ![]() cosθ),
cosθ),
所以圆C的直角坐标方程为:x2+y2+2x﹣2 ![]() y=0
y=0
(2)解:设z= ![]() x+y
x+y
由圆C的方程x2+y2+2x﹣2 ![]() y=0,可得(x+1)2+(y﹣
y=0,可得(x+1)2+(y﹣ ![]() )2=4
)2=4
所以圆C的圆心是(﹣1, ![]() ),半径是2
),半径是2
将  代入z=
代入z= ![]() x+y得z=﹣t
x+y得z=﹣t
又直线l过C(﹣1, ![]() ),圆C的半径是2,
),圆C的半径是2,
由题意有:﹣2≤t≤2
所以﹣2≤t≤2
即 ![]() x+y的取值范围是[﹣2,2]
x+y的取值范围是[﹣2,2]
【解析】(1)利用极坐标与直角坐标的方程互化的方法,可得圆C的直角坐标方程;(2)将  代入z=
代入z= ![]() x+y得z=﹣t,又直线l过C(﹣1,
x+y得z=﹣t,又直线l过C(﹣1, ![]() ),圆C的半径是2,可得结论.
),圆C的半径是2,可得结论.
【考点精析】利用直线的参数方程对题目进行判断即可得到答案,需要熟知经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为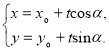 (
(![]() 为参数).
为参数).

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目