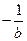题目内容
已知集合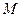 是满足下列性质的函数
是满足下列性质的函数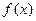 的全体:存在非零常数
的全体:存在非零常数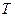 ,对任意
,对任意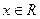 ,有
,有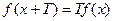 成立。
成立。
(1)函数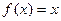 是否属于集合
是否属于集合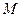 ?说明理由;
?说明理由;
(2)设函数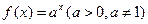 的图象与
的图象与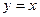 的图象有公共点,证明:
的图象有公共点,证明:
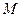 是满足下列性质的函数
是满足下列性质的函数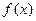 的全体:存在非零常数
的全体:存在非零常数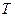 ,对任意
,对任意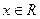 ,有
,有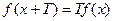 成立。
成立。(1)函数
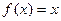 是否属于集合
是否属于集合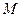 ?说明理由;
?说明理由;(2)设函数
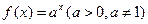 的图象与
的图象与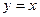 的图象有公共点,证明:
的图象有公共点,证明:
略
(1)对于非零常数T,f(x+T)=x+T, Tf(x)=Tx. 因为对任意x∈R,x+T= Tx不能恒成立,所以f(x)=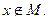
(2)因为函数f(x)=ax(a>0且a≠1)的图象与函数y=x的图象有公共点,
所以方程组: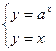 有解,消去y得ax=x,
有解,消去y得ax=x,
显然x=0不是方程ax=x的解,所以存在非零常数T,使aT="T."
于是对于f(x)=ax有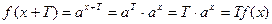 故f(x)=ax∈M.
故f(x)=ax∈M.
(2)因为函数f(x)=ax(a>0且a≠1)的图象与函数y=x的图象有公共点,
所以方程组:
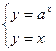 有解,消去y得ax=x,
有解,消去y得ax=x,显然x=0不是方程ax=x的解,所以存在非零常数T,使aT="T."
于是对于f(x)=ax有
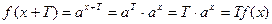 故f(x)=ax∈M.
故f(x)=ax∈M.
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 的曲线.
的曲线.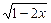 的值域是( )
的值域是( )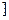
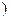
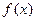 是定义在
是定义在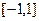 上的奇函数,且
上的奇函数,且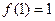 ,若
,若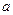 、
、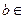
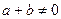 ,有
,有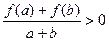 ;
;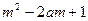 对所有的
对所有的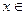
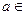
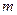 的取值范围。
的取值范围。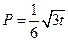 ,
,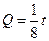 .今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).
.今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).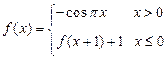 ,则
,则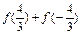 的值等于
的值等于 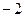
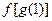 相同的是( )
相同的是( )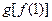 ;
;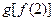 ;
;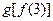 ;
;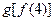
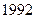 年底世界人口达到
年底世界人口达到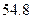 亿,若人口的年平均增长率为
亿,若人口的年平均增长率为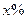 ,
,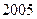 年底世界人口
年底世界人口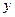 亿,那么
亿,那么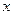 的函数关系式为 .
的函数关系式为 .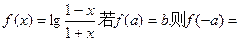 ( )
( )
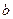 B
B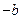 C
C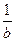 D
D