题目内容
抛物线y2=2px(p>0)上纵坐标为-p的点M到焦点的距离为2.
(Ⅰ)求p的值;
(Ⅱ)如图,A,B,C为抛物线上三点,且线段MA,MB,MC 与x轴交点的横坐标依次组成公差为1的等差数列,若△AMB的面积是△BMC面积的 ,求直线MB的方程.
,求直线MB的方程.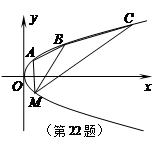
(Ⅰ)求p的值;
(Ⅱ)如图,A,B,C为抛物线上三点,且线段MA,MB,MC 与x轴交点的横坐标依次组成公差为1的等差数列,若△AMB的面积是△BMC面积的
 ,求直线MB的方程.
,求直线MB的方程.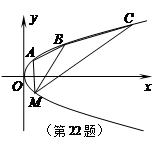
(本题15分):(Ⅰ)解:设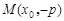 , 则
, 则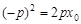 ,
,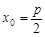 ,
,
由抛物线定义,得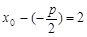 所以
所以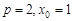 . ……5分
. ……5分
(Ⅱ)由(Ⅰ)知抛物线方程为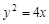 ,
,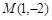 .
.
设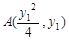 ,
,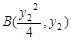 ,
,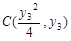 (
(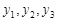 均大于零) ……6分
均大于零) ……6分
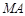 ,
, ,
,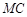 与
与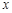 轴交点的横坐标依次为
轴交点的横坐标依次为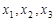 .
.
(1)当
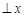 轴时,直线
轴时,直线 的方程为
的方程为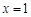 ,则
,则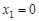 ,不合题意,舍去.……7分
,不合题意,舍去.……7分
(2) 与
与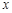 轴不垂直时,
轴不垂直时,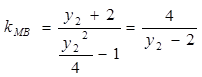 ,
,
设直线 的方程为
的方程为 ,即
,即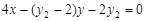 ,
,
令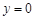 得2
得2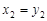 ,同理2
,同理2 ,2
,2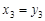 , ……10分
, ……10分
因为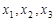 依次组成公差为1的等差数列,
依次组成公差为1的等差数列,
所以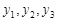 组成公差为2的等差数列. ……12分
组成公差为2的等差数列. ……12分
设点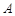 到直线
到直线 的距离为
的距离为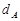 ,点
,点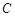 到直线
到直线 的距离为
的距离为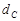 ,
,
因为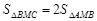 ,所以
,所以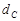 =2
=2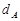 ,
,
所以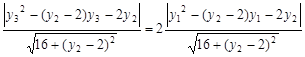 ……14分
……14分
得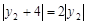 ,即
,即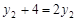 ,所以
,所以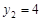 ,
,
所以直线 的方程为:
的方程为: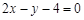 ……15分
……15分
解法二:(Ⅰ)同上. (Ⅱ)由(Ⅰ)知抛物线方程为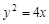 ,
,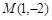 .
.
由题意,设
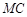 与
与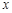 轴交点的横坐标依次为
轴交点的横坐标依次为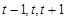
设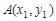 ,
,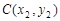 (
(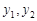 均大于零). ……6分
均大于零). ……6分
(1)当
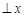 轴时,直线
轴时,直线 的方程为
的方程为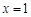 ,则
,则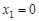 ,不合题意,舍去. ……7分
,不合题意,舍去. ……7分
(2) 与
与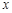 轴不垂直时,
轴不垂直时,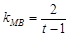
设直线 的方程为
的方程为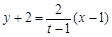 ,即
,即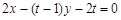 ,
,
同理直线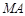 的方程为
的方程为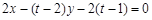 ,
,
由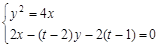 得
得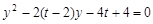
则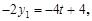 所以
所以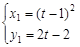 , ……12分
, ……12分
同理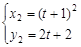 ,设点
,设点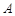 到直线
到直线 的距离为
的距离为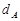 ,点
,点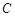 到直线
到直线 的距离为
的距离为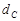 , 因为
, 因为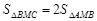 ,所以
,所以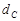 =2
=2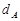 ,
,
所以 ……14分
……14分
化简得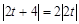 ,即
,即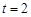 ,
,
所以直线 的方程为:
的方程为: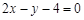 ……15分
……15分
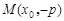 , 则
, 则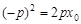 ,
,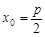 ,
,由抛物线定义,得
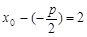 所以
所以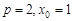 . ……5分
. ……5分(Ⅱ)由(Ⅰ)知抛物线方程为
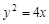 ,
,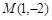 .
.设
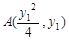 ,
,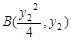 ,
,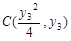 (
(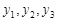 均大于零) ……6分
均大于零) ……6分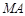 ,
, ,
,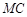 与
与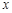 轴交点的横坐标依次为
轴交点的横坐标依次为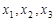 .
.(1)当

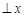 轴时,直线
轴时,直线 的方程为
的方程为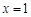 ,则
,则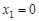 ,不合题意,舍去.……7分
,不合题意,舍去.……7分(2)
 与
与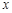 轴不垂直时,
轴不垂直时,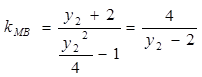 ,
,设直线
 的方程为
的方程为 ,即
,即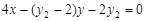 ,
,令
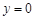 得2
得2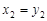 ,同理2
,同理2 ,2
,2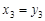 , ……10分
, ……10分因为
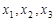 依次组成公差为1的等差数列,
依次组成公差为1的等差数列,所以
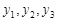 组成公差为2的等差数列. ……12分
组成公差为2的等差数列. ……12分设点
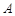 到直线
到直线 的距离为
的距离为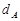 ,点
,点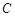 到直线
到直线 的距离为
的距离为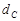 ,
,因为
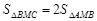 ,所以
,所以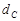 =2
=2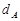 ,
,所以
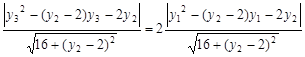 ……14分
……14分得
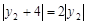 ,即
,即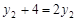 ,所以
,所以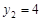 ,
,所以直线
 的方程为:
的方程为: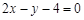 ……15分
……15分解法二:(Ⅰ)同上. (Ⅱ)由(Ⅰ)知抛物线方程为
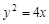 ,
,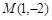 .
.由题意,设
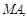
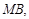
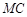 与
与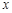 轴交点的横坐标依次为
轴交点的横坐标依次为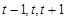
设
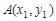 ,
,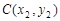 (
(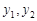 均大于零). ……6分
均大于零). ……6分(1)当

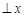 轴时,直线
轴时,直线 的方程为
的方程为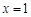 ,则
,则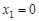 ,不合题意,舍去. ……7分
,不合题意,舍去. ……7分(2)
 与
与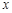 轴不垂直时,
轴不垂直时,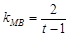
设直线
 的方程为
的方程为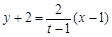 ,即
,即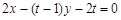 ,
,同理直线
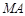 的方程为
的方程为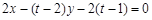 ,
,由
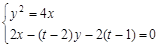 得
得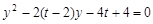
则
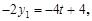 所以
所以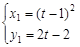 , ……12分
, ……12分同理
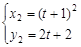 ,设点
,设点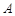 到直线
到直线 的距离为
的距离为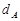 ,点
,点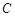 到直线
到直线 的距离为
的距离为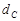 , 因为
, 因为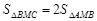 ,所以
,所以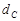 =2
=2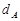 ,
,所以
 ……14分
……14分化简得
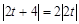 ,即
,即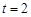 ,
,所以直线
 的方程为:
的方程为: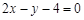 ……15分
……15分略

练习册系列答案
相关题目
 经过抛物线
经过抛物线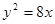 的焦点
的焦点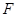 ,且与抛物线相交于
,且与抛物线相交于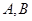 两点,求线段
两点,求线段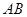 的长。
的长。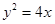 上一点
上一点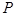 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为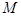 ,且
,且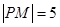 ,设抛物线的焦点为
,设抛物线的焦点为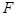 ,则
,则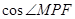 = .
= .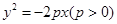 上,则它的边长为( )
上,则它的边长为( )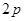


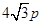
 的焦点坐标是 ( )
的焦点坐标是 ( )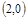

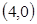

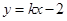 交抛物线
交抛物线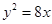 于A,B两点,若AB中点的横坐标是2,
于A,B两点,若AB中点的横坐标是2,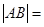 _
_ 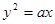 的准线是直线
的准线是直线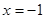 ,那么它的焦点坐标是 ( )
,那么它的焦点坐标是 ( )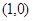



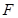 是抛物线
是抛物线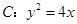 的焦点,过
的焦点,过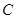 于
于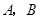 两点.则
两点.则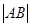 的值等于 .
的值等于 . 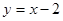 与抛物线
与抛物线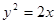 相交于
相交于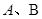 两点,
两点, 为坐标原点,则
为坐标原点,则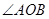 = .
= .