题目内容
(本题满分12分)
斜率为2的直线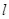 经过抛物线
经过抛物线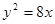 的焦点
的焦点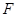 ,且与抛物线相交于
,且与抛物线相交于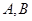 两点,求线段
两点,求线段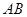 的长。
的长。
斜率为2的直线
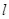 经过抛物线
经过抛物线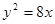 的焦点
的焦点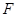 ,且与抛物线相交于
,且与抛物线相交于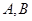 两点,求线段
两点,求线段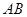 的长。
的长。 .
.本试题主要是考查了利用抛物线的性质和抛物线的定义结合焦点弦公式可知|AB|的长为 xA+xB+4。这样利用直线方程与抛物线方程联立方程组,得到韦达定理中的根与系数的关系可知结论。
解:抛物线y2=8x的焦点F(2,0),准线方程为x=-2
∴直线AB的方程为y=2(x-2)
联立方程 y=2(x-2)与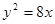
可得x2-8x+4=0
∴xA+xB=8,xA•xB=4
(法一):由抛物线的定义可知,AB=AF+BF=xA+2+xB+2=xA+xB+4=10

解:抛物线y2=8x的焦点F(2,0),准线方程为x=-2
∴直线AB的方程为y=2(x-2)
联立方程 y=2(x-2)与
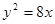
可得x2-8x+4=0
∴xA+xB=8,xA•xB=4
(法一):由抛物线的定义可知,AB=AF+BF=xA+2+xB+2=xA+xB+4=10


练习册系列答案
相关题目
 上一点
上一点 到其焦点的距离为5.
到其焦点的距离为5. 与
与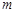 的值;
的值; 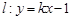 与抛物线
与抛物线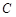 相交于
相交于 、
、 两点,
两点, 、
、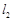 分别是该抛物线在
分别是该抛物线在 、
、 分别是
分别是
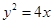 上任意一点
上任意一点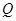 ,点
,点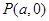 都满足
都满足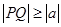 ,则
,则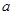 的取值范围是___.
的取值范围是___.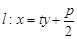 与抛物线
与抛物线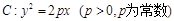 交于不同两点
交于不同两点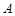 、
、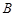 ,点
,点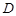 为抛物线准线上的一点。
为抛物线准线上的一点。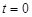 ,且三角形
,且三角形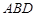 的面积为4,求抛物线的方程;
的面积为4,求抛物线的方程;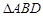 为正三角形时,求出点
为正三角形时,求出点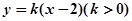 与抛物线
与抛物线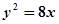 相交于
相交于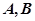 两点,
两点,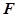 为抛物线的焦点,若
为抛物线的焦点,若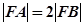 ,则
,则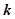 的值为 ______________.
的值为 ______________.
 的焦点为
的焦点为 ,过
,过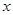 轴的直线与抛物线交于
轴的直线与抛物线交于 两点,已知
两点,已知 .
. 的方程;
的方程; ,过点
,过点 作方向向量为
作方向向量为 的直线与抛物线
的直线与抛物线 两点,求使
两点,求使 为钝角时实数
为钝角时实数 的取值范围;
的取值范围;
 ,过
,过 为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。
为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。 ,过
,过 ,求直线MB的方程.
,求直线MB的方程.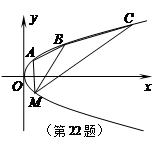
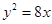 的焦点坐标是
的焦点坐标是 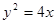 的焦点作一直线交抛物线于A(x1, y1)、B(x2, y2)两点,并且已知
的焦点作一直线交抛物线于A(x1, y1)、B(x2, y2)两点,并且已知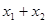 =6,那么
=6,那么 =( )
=( )