题目内容
3.以双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点A为圆心作与渐近线相切的圆,过左焦点F作该圆的切线,设切点为P,切线与y轴的交点为M,且FM:MP=8:3,求双曲线的离心率.分析 由题意可推出FM=$\frac{8}{11}$FP,从而可得FP=$\sqrt{\frac{11}{8}(a+c)c}$,再求得r=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$,从而利用勾股定理可得(a+c)2=$\frac{11}{8}$(a+c)c+$\frac{{a}^{2}{b}^{2}}{{c}^{2}}$;从而解得.
解答 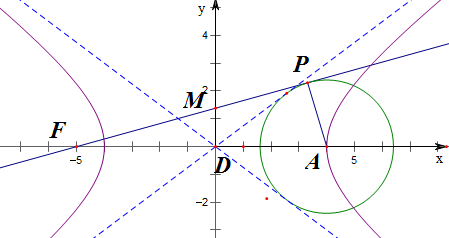 解:∵$\frac{FM}{MP}$=$\frac{8}{3}$,
解:∵$\frac{FM}{MP}$=$\frac{8}{3}$,
∴$\frac{FM}{FP}$=$\frac{8}{11}$,
即FM=$\frac{8}{11}$FP;
又∵△FMD∽△FAP,
∴$\frac{FD}{FP}$=$\frac{FM}{FA}$,
∴FP=$\sqrt{\frac{11}{8}(a+c)c}$,
A(a,0),
∴r=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$,
又∵FA2=FP2+PA2,
∴(a+c)2=$\frac{11}{8}$(a+c)c+$\frac{{a}^{2}{b}^{2}}{{c}^{2}}$;
即3e4-5e3-8=(e+1)(e-2)(3e2-2e+4)=0,
解得,e=-1(舍去)或e=2;
故双曲线的离心率为2.
点评 本题考查了双曲线的性质及应用,化简比较困难,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
11.一个算法的程序框图如图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )


| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |
8.已知抛物线y2=4x的准线与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的一条准线重合,则这条抛物线y2=4x与双曲线$\frac{x^2}{3}-\frac{y^2}{b^2}=1$的交点P到抛物线焦点的距离为( )
| A. | $\sqrt{21}$ | B. | 21 | C. | 6 | D. | 4 |
12.抛物线y=$\frac{1}{8}$x2上到焦点的距离等于10的点的坐标为( )
| A. | (-8,8) | B. | (8,8) | C. | (-8,-8)或(8,-8) | D. | (-8,8)或(8,8) |