题目内容
15.在△ABC中,角A,B,C所对的边分别为a,b,c,且a2+b2=ab+c2.(Ⅰ)求角C的值;
(Ⅱ)若$c=\sqrt{3}$,求S△ABC的最大值.
分析 (Ⅰ)根据余弦定理化简已知的式子,求出cosB和角B的值;
(Ⅱ)根据余弦定理和条件可得3=a2+b2-ab,利用基本不等式求出ab的范围,代入三角形的面积公式即可S△ABC的最大值.
解答 解:(I)由a2+b2=ab+c2可得,a2+b2-c2=ab,
根据余弦定理得,$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{1}{2}$,…(3分)
又0<C<π,则$C=\frac{π}{3}$; …(5分)
(II)由余弦定理得,c2=a2+b2-2abcosC,
则3=a2+b2-ab,即 ab+3=a2+b2≥2ab …(7分)
解得ab≤3,…(8分)
因为${S_{△ABC}}=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{4}ab$,…(10分)
所以${S_{△ABC}}≤\frac{{3\sqrt{3}}}{4}$,…(11分)
当且仅当a=b=$\sqrt{3}$时取等号,…(12分)
故S△ABC的最大值是$\frac{{3\sqrt{3}}}{4}$. …(13分)
点评 本题考查了余弦定理,三角形的面积公式,以及基本不等式的应用,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.执行如图所示的程序框图,若输出的y=$\frac{1}{2}$,则输入的x的值可能为( )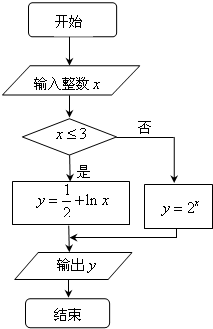

| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
20.由曲线y=x2,y=x围成的封闭图形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
4.如图是一个算法的流程图,则输出S的值是( )
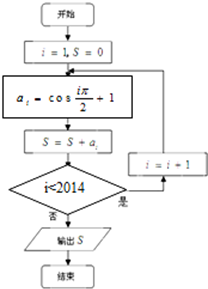

| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |