题目内容
(本小题满分14分)
抛物线D以双曲线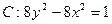 的焦点
的焦点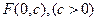 为焦点
为焦点 .
.
(1)求抛物线D的 标准方程;
标准方程;
(2)过直线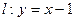 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐 标;
标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
抛物线D以双曲线
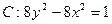 的焦点
的焦点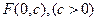 为焦点
为焦点 .
.(1)求抛物线D的
 标准方程;
标准方程;(2)过直线
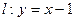 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐 标;
标;(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
解:(1)由题意,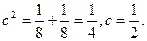
所以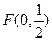 ,抛物线D的标准方程为
,抛物线D的标准方程为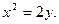 …………3分
…………3分
(2)设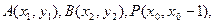 由
由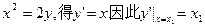
抛物线D在点A处的切线方程为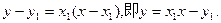 …………4分
…………4分
而A点处的 切线过点
切线过点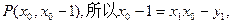 即
即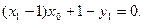
同理,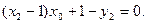 可见,点A,B在直线
可见,点A,B在直线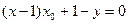 上.
上.
令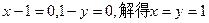 所以,直线AB过定点Q(1,1) …………6分
所以,直线AB过定点Q(1,1) …………6分
(3)设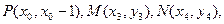 直线PQ的方程为
直线PQ的方程为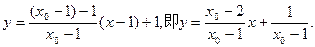
由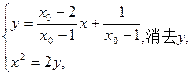 得
得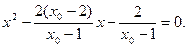
由韦达定理,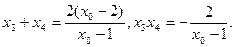 …………9分
…………9分
而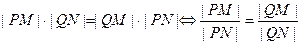
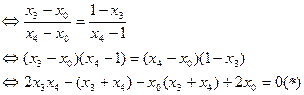
…………12分
将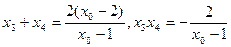 代入方程(*)的左边,得
代入方程(*)的左边,得
(*)的左边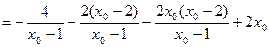
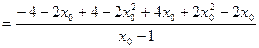 =0
=0
因而有|PM|·|QN|=|QM|·|PN|. …………14分
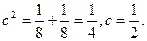
所以
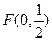 ,抛物线D的标准方程为
,抛物线D的标准方程为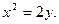 …………3分
…………3分(2)设
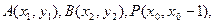 由
由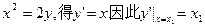
抛物线D在点A处的切线方程为
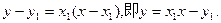 …………4分
…………4分而A点处的
 切线过点
切线过点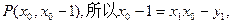 即
即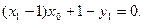
同理,
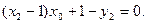 可见,点A,B在直线
可见,点A,B在直线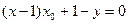 上.
上.令
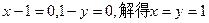 所以,直线AB过定点Q(1,1) …………6分
所以,直线AB过定点Q(1,1) …………6分
|
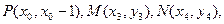 直线PQ的方程为
直线PQ的方程为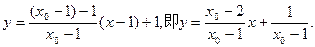
由
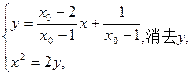 得
得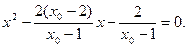
由韦达定理,
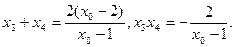 …………9分
…………9分而
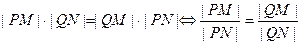
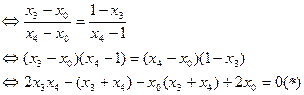
…………12分
将
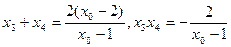 代入方程(*)的左边,得
代入方程(*)的左边,得(*)的左边
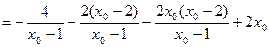
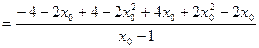 =0
=0因而有|PM|·|QN|=|QM|·|PN|. …………14分
略

练习册系列答案
相关题目
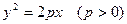 上有一点
上有一点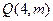 到焦点
到焦点 的距离为5,
的距离为5,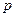 及
及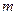 的值。
的值。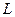 交抛物线于A,B两点,若
交抛物线于A,B两点,若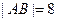 ,求直线
,求直线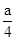
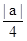
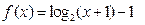 的零点是抛物线
的零点是抛物线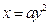 焦点的横坐标,则
焦点的横坐标,则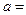
 .
.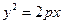 (
(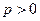 )的焦点F作倾斜角为450的直线交抛物线于A,B两点,若|AB|=4,则
)的焦点F作倾斜角为450的直线交抛物线于A,B两点,若|AB|=4,则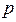 的值为( )
的值为( )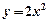 的准线方程是_____________;
的准线方程是_____________;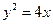 的焦点为圆心,且过坐标原点的圆的方程为
的焦点为圆心,且过坐标原点的圆的方程为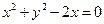

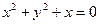

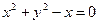
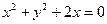
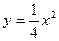 ,则准线方程为 ( )
,则准线方程为 ( )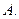
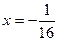
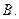
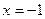
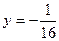
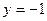
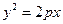 的焦点与双曲线
的焦点与双曲线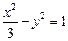 的右焦点重合,则
的右焦点重合,则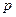 的值为( )
的值为( )