Question

【题目】已知定义在R上的偶函数f（x）满足f（x+1）=﹣f（x），且当x∈[﹣1，0]时， ，函数 ，则关于x的不等式f（x）＜g（x）的解集为（ ）
A.（﹣2，﹣1）∪（﹣1，0）
B.
C.
D.

Answer 1

【答案】D
【解析】解：由题意知，f（x+1）=﹣f（x），

∴f（x+2）=﹣f（x+1）=f（x），

即函数f（x）是周期为2的周期函数．

若x∈[0，1]时，﹣x∈[﹣1，0]，

∵当x∈[﹣1，0]时， ，

∴当x∈[0，1]时， ，

∵f（x）是偶函数，∴f（x）= ，

即f（x）= ．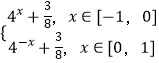

∵函数 ，

∴g（x）= ，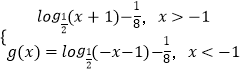

作出函数f（x）和g（x）的图象如图：

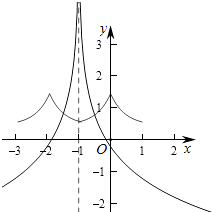
当﹣1＜x＜0时，由 = ，

则 ，由选项验证解得x= ，

即此时不等式式f（x）＜g（|x+1|）的解为﹣1＜x＜ ，

∵函数g（x）关于x=﹣1对称，

∴不等式式f（x）＜g（x）的解为﹣1＜x＜ 或 ＜x＜﹣1，

即不等式的解集为（ ，﹣1）∪（﹣1， ），

故选：D．

【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点，需要掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题．