题目内容
【题目】设命题![]() :实数
:实数![]() 满足
满足![]() (其中
(其中![]() ),命题
),命题![]() :实数
:实数![]() 满足
满足![]()
(1)若![]() ,且
,且![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)当a=1时,解得1<x<4,得到当p为真时,实数x的取值范围是1<x<4.当q为真时,解得2<x≤5,进而根据p∧q为真,即可求解;
(2)由![]() 是
是![]() 的必要不充分条件,即p是q的必要不充分条件,即
的必要不充分条件,即p是q的必要不充分条件,即![]() 且
且![]() ,根据集合的运算即可求解.
,根据集合的运算即可求解.
(1)当a=1时,x2-5ax+4a2<0即为x2-5x+4<0,解得1<x<4,
当p为真时,实数x的取值范围是1<x<4.当q为真时,由![]() ,知2<x≤5.
,知2<x≤5.
若p∧q为真,则p真且q真,所以实数x的取值范围是(2,4).
(2)![]() 是
是![]() 的必要不充分条件,即p是q的必要不充分条件.
的必要不充分条件,即p是q的必要不充分条件.
设A={x|p(x)},B={x|q(x)},则![]() 且
且![]() .由x2-5ax+4a2<0得(x-4a)(x-a)<0,∵a>0,∴A={x|a<x<4a},又B={x|2<x≤5},则a≤2且4a>5,解得
.由x2-5ax+4a2<0得(x-4a)(x-a)<0,∵a>0,∴A={x|a<x<4a},又B={x|2<x≤5},则a≤2且4a>5,解得![]() <a≤2.
<a≤2.
∴实数a的取值范围是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史。某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位; ![]() )数据,将数据分组如下表:
)数据,将数据分组如下表:
分组 | 频数 | 频率 |
| 4 | |
| 26 | |
| ||
| 28 | |
| 10 | |
| 2 | |
合计 | 100 |
(1)在答题卡上完成频率分布表;
(2)以表中的频率作为概率,估计重量落在![]() 中的概率及重量小于2.45的概率是多少?
中的概率及重量小于2.45的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力,某移动支付公司在我市随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果认为每周使用移动支付超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过![]() 的前提下,认为是否“喜欢使用移动支付”与性别有关?
的前提下,认为是否“喜欢使用移动支付”与性别有关?
(2)每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户,
①求抽取的4名用户中,既有男“移动支付达人”又有女“移动支付达人”的概率;
②为了鼓励女性用户使用移动支付,对抽出的女“移动支付达人”每人奖励500元,记奖励总金额为![]() ,求
,求![]() 的数学期望.
的数学期望.
附表及公式:
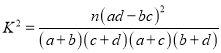
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|