题目内容
【题目】《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知![]() 三人分配奖金的衰分比为
三人分配奖金的衰分比为![]() ,若
,若![]() 分得奖金1000元,则
分得奖金1000元,则![]() 所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
A.![]() ,12800元B.
,12800元B.![]() ,12800元
,12800元
C.![]() ,10240元D.
,10240元D.![]() ,10240元
,10240元
【答案】A
【解析】
由题意得甲、乙、丙、丁获得奖金组成等比数列![]() ,设“衰分比”为
,设“衰分比”为![]() ,则数列的公比为
,则数列的公比为![]() ,而由题意可知
,而由题意可知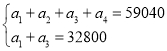 ,进而计算可得
,进而计算可得![]() 的值.
的值.
解:由题意设,甲、乙、丙、丁获得奖金组成等比数列![]() ,设“衰分比”为
,设“衰分比”为![]() ,则数列的公比为
,则数列的公比为![]() ,则有
,则有
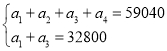
则有![]() ,
,![]() ,
,
解得 ![]() ,则
,则![]() ,
,
因为![]()
所以![]() ,解得
,解得![]()
故选:A

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)具有较强的相关性,且两者之间有如下对应数据:
(单位:万元)具有较强的相关性,且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中的线性回归方程,当广告费支出为10万元时,预测销售额是多少?
参考数据: ![]() ,
,![]() ,
,![]() 。
。
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.