题目内容
4.正四面体ABCD的棱长为a,EFG分别是AB,AC,CD的中点,截面EFG交棱BD于H则点A到截面EFGH的距离是$\frac{\sqrt{2}}{2}a$.分析 由题意画出图形,把A到截面的距离转化为AD的中点到截面的距离,进一步转化为求AD,BC的中点间的距离得答案.
解答 解:如图, ∵ABCD是正四面体,且E,F,G分别是AB,AC,CD的中点,
∵ABCD是正四面体,且E,F,G分别是AB,AC,CD的中点,
可得四边形EFGH为正方形,取AD中点M,BC中点N,连接MN,
则有MN⊥平面EFGH,且M,N到平面EFGH的距离相等,
BM=CM=$\frac{\sqrt{3}}{2}a$,则MN=$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}-(\frac{1}{2}a)^{2}}=\frac{\sqrt{2}}{2}a$.
∴M到平面EFGH的距离为$\frac{\sqrt{2}}{2}a$.
∵AD∥平面EFGH,∴A到平面EFGH的距离为$\frac{\sqrt{2}}{2}a$.
故答案为:$\frac{\sqrt{2}}{2}a$.
点评 本题考查了棱锥的结构特征,考查了空间直线和平面的位置关系,是基础的计算题.

练习册系列答案
相关题目
12.如图所示,PA=PB=PC,且它们所成的角均为60°,则二面角B-PA-C的余弦值是( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.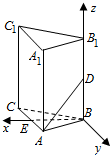 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )
 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | -$\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | -$\frac{{\sqrt{10}}}{4}$ |
13. 一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图如图所示:老板根据销售量给以店员奖励,具体奖励规定如表:
一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图如图所示:老板根据销售量给以店员奖励,具体奖励规定如表:
(1)求在未来连续3天里,店员共获得奖励150元的概率
(2)记未来连续2天,店员获得奖励X元,求随机变量X的分布列及数学期望EX.
 一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图如图所示:老板根据销售量给以店员奖励,具体奖励规定如表:
一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图如图所示:老板根据销售量给以店员奖励,具体奖励规定如表:| 销售量X个 | X<100 | 100≤X<150 | 150≤X<200 | X≥200 |
| 奖励金额(元) | 0 | 50 | 100 | 150 |
(2)记未来连续2天,店员获得奖励X元,求随机变量X的分布列及数学期望EX.
14.△ABC的内角A,B,C的对边分别为a,b,c,若a,b,c,成等比数列,且c=2a,则cosC=( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
 在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为A1D1和A1B1的中点.
在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1的棱长为2,E,F分别为A1D1和A1B1的中点. 如图,空间四边形ABCD中,AB⊥CD,DE是AB与CD的公垂线段,且 AE=BE=DE.
如图,空间四边形ABCD中,AB⊥CD,DE是AB与CD的公垂线段,且 AE=BE=DE.