题目内容
19．
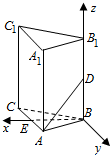在正三棱柱ABC-A1B1C1中，已知AB=1，D在棱BB1上，且BD=1，则AD与平面ACC1A1所成的角的正弦值为（ ）| A． | $\frac{{\sqrt{6}}}{4}$ | B． | -$\frac{{\sqrt{6}}}{4}$ | C． | $\frac{{\sqrt{10}}}{4}$ | D． | -$\frac{{\sqrt{10}}}{4}$ |
分析 根据题意画出图形，过B作BF⊥AC，过B1作B1E⊥A1C1，连接EF，过D作DG⊥EF，连接AG，证明DG⊥面AA1C1C，∠DAG=α，解直角三角形ADG即可．
解答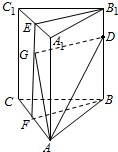 
解：如图所示，过B作BF⊥AC，过B1作B1E⊥A1C1，连接EF，过D作DG⊥EF，连接AG，
在正三棱柱中，有B1E⊥AA1C1C，BF⊥面AA1C1C，
故DG⊥面AA1C1C，
∴∠DAG=α，可求得DG=BF=$\frac{\sqrt{3}}{2}$，
AG=$\sqrt{A{F}^{2}+F{G}^{2}}$=$\frac{\sqrt{5}}{2}$，AD=$\sqrt{\frac{3}{4}+\frac{5}{4}}$=$\sqrt{2}$
故sinα=$\frac{\sqrt{6}}{4}$
故选：A．
点评 考查直线和平面所成的角，关键是找到斜线在平面内的射影，把空间角转化为平面角求解，属基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图，在正三棱柱中，AB=2，AA1=2，由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M，求：
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA=30°，PA=AB=2，点E为线段PB的中点，点M在$\widehat{AB}$上，且OM∥AC．
11．
在直三棱柱ABC-A1B1C1中，∠ACB=90°，CA=CB=CC1=1，则直线A1B与平面BB1C1C所成角的正弦值为（ ）
在直三棱柱ABC-A1B1C1中，∠ACB=90°，CA=CB=CC1=1，则直线A1B与平面BB1C1C所成角的正弦值为（ ）| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{15}}}{5}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
