题目内容
12.如图所示,PA=PB=PC,且它们所成的角均为60°,则二面角B-PA-C的余弦值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 取PA=PB=PC=2,PE=1,连接BE,CE,运用题目的条件得出∠BEC为二面角B-PA-C的平面角,△BEC中,BE=CE=$\sqrt{3}$,BC=2,运用余弦定理求解即可.
解答 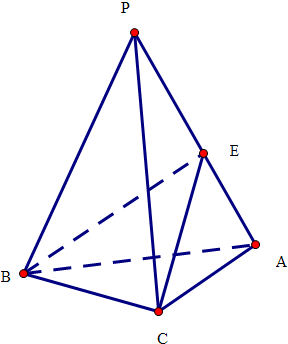 解:取PA=PB=PC=2,PE=1,连接BE,CE
解:取PA=PB=PC=2,PE=1,连接BE,CE
∵∠BPE=∠CPE=60°,
∴△PBE≌△PCE,
∴BE=CE,
根据余弦定理得出:BE=CE=$\sqrt{3}$,
∴根据勾股定理判断出BE⊥PE,CE⊥PE,
∠BEC为二面角B-PA-C的平面角,
∵△BEC中,BE=CE=$\sqrt{3}$,BC=2,
∴cos∠BEC=$\frac{3+3-4}{2×\sqrt{3}×\sqrt{3}}$=$\frac{1}{3}$,
故选:B
点评 本题考查的知识点是二面角的平面角及求法,其中求出二面角的平面角转化为三角形中求解是解答本题的关键.

练习册系列答案
相关题目
12. 如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )
如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )
 如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )
如图,正三棱锥A-BCD中,E、F分别为BD、AD的中点,且EF⊥CF,底面边长为2,则点B到平面ACD的距离为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
2.已知复数z满足z(1+i)=1(其中i为虚数单位),则z的共轭复数是( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1+i}{2}$ | D. | $\frac{-1-i}{2}$ |
 如图,四棱锥P-ABCD中,底面ABCD为正方形,PA=PD,PA⊥平面PDC,
如图,四棱锥P-ABCD中,底面ABCD为正方形,PA=PD,PA⊥平面PDC,
 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC. 如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2
如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,E是PC的中点.