题目内容
16. 如图,空间四边形ABCD中,AB⊥CD,DE是AB与CD的公垂线段,且 AE=BE=DE.
如图,空间四边形ABCD中,AB⊥CD,DE是AB与CD的公垂线段,且 AE=BE=DE.(1)证明:AC⊥BD;
(2)若∠ACB=60°,求直线BD与平面ABC所成的角的大小.
分析 (1)证明CD⊥平面ABD,AD⊥BD,即可证明AC⊥BD;
(2)连结CE,作DH⊥CE于H,连结BH,确定BD与平面ABC所成的角为∠DBH,即可求直线BD与平面ABC所成的角的大小.
解答 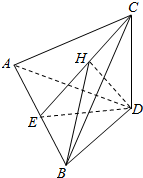 (1)证明:由已知AB⊥CD,DE⊥CD,AB∩DE=E,
(1)证明:由已知AB⊥CD,DE⊥CD,AB∩DE=E,
可得CD⊥平面ABD.
又△ABD中,AE=BE=DE,DE⊥AB,
∴AD=BD,AD⊥BD,
又AD为AC在平面ABD内的射影,
∴AC⊥BD;
(2)解:连结CE,作DH⊥CE于H,连结BH.
由AB⊥DE,AB⊥CD知,AB⊥平面CDE,
∴平面ABC⊥平面CDE,
又DH⊥CE,∴DH⊥平面ABC,
故BD与平面ABC所成的角为∠DBH.
∵Rt△CAD≌Rt△CBD,
∴AC=BC,
又∠ACB=60°,
∴△ABC为等边三角形.
记AB=a,则CE=$\frac{\sqrt{3}}{2}$a,DE=$\frac{1}{2}$a,BD=$\frac{\sqrt{2}}{2}$a.
在Rt△CDE中,CD=$\frac{\sqrt{2}}{2}$a,∴DH=$\frac{CD•DE}{CE}$=$\frac{\sqrt{6}}{6}$a,
故在Rt△BDH中,sin∠DBH=$\frac{\sqrt{3}}{3}$,
故BD与平面ABC所成的角为arcsin$\frac{\sqrt{3}}{3}$.
点评 本题考查线面垂直的判定与性质,考查线面角,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
11. 在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为( )
在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为( )
 在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为( )
在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{15}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,E是PC的中点.
 一个几何体的三视图(单位:m),则该几何体的体积为44m3.
一个几何体的三视图(单位:m),则该几何体的体积为44m3. 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,且|F1F2|=2,动直线l:y=kx+m与椭圆C有且仅有一个公共点.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,且|F1F2|=2,动直线l:y=kx+m与椭圆C有且仅有一个公共点.