题目内容
【题目】已知函数f(x)=x﹣a,g(x)=a|x|,a∈R.
(1)设F(x)=f(x)﹣g(x). ①若a= ![]() ,求函数y=F(x)的零点;
,求函数y=F(x)的零点;
②若函数y=F(x)存在零点,求a的取值范围.
(2)设h(x)=f(x)+g(x),x∈[﹣2,2],若对任意x1 , x2∈[﹣2,2],|h(x1)﹣h(x2)|≤6恒成立,试求a的取值范围.
【答案】
(1)解:F(x)=f(x)﹣g(x)=x﹣a﹣a|x|,
①若a= ![]() ,则由F(x)=x﹣
,则由F(x)=x﹣ ![]() |x|﹣
|x|﹣ ![]() =0得:
=0得: ![]() |x|=x﹣
|x|=x﹣ ![]() ,
,
当x≥0时,解得:x=1;
当x<0时,解得:x= ![]() (舍去);
(舍去);
综上可知,a= ![]() 时,函数y=F(x)的零点为1;
时,函数y=F(x)的零点为1;
②若函数y=F(x)存在零点,则x﹣a=a|x|,
当a>0时,作图如下:
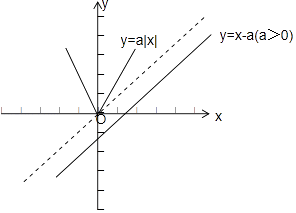
由图可知,当0<a<1时,折线y=a|x|与直线y=x﹣a有交点,即函数y=F(x)存在零点;
同理可得,当﹣1<a<0时,求数y=F(x)存在零点;
又当a=0时,y=x与y=0有交点(0,0),函数y=F(x)存在零点;
综上所述,a的取值范围为(﹣1,1).
(2)∵h(x)=f(x)+g(x)=x-a+a|x|,x∈[-2,2], ∴当-2≤x<0时,h(x)=(1-a)x-a; 当0≤x≤2时,h(x)=(1+a)x-a; 又对任意x1,x2∈[-2,2],|h(x1)-h(x2)|≤6恒成立, 则h(x1)max-h(x2)min≤6, ①当a≤-1时,1-a>0,1+a≤0,h(x)=(1-a)x-a在区间[-2,0)上单调递增; h(x)=(1+a)x-a在区间[0,2]上单调递减(当a=-1时,h(x)=-a); ∴h(x)max=h(0)=-a,又h(-2)=a-2,h(2)=2+a, ∴h(x2)min=h(-2)=a-2, ∴-a-(a-2)=2-2a≤6,解得a≥-2, 综上,-2≤a≤-1; ②当-1<a<1时,1-a>0,1-a>0,∴h(x)=(1-a)x-a在区间[-2,0)上单调递增, 且h(x)=(1+a)x-a在区间[0,2]上也单调递增, ∴h(x)max=h(2)=2+a,h(x2)min=h(-2)=a-2, 由a+2-(a-2)=4≤6恒成立,即-1<a<1适合题意; ③当a≥1时,1-a≤0,1+a>0,h(x)=(1-a)x-a在区间[-2,0)上单调递减 (当a=1时,h(x)=-a),h(x)=(1+a)x-a在区间[0,2]上单调递增; ∴h(x)min=h(0)=-a; 又h(2)=2+a>a-2=h(-2), ∴h(x)max=h(2)=2+a, ∴2+a-(-a)=2+2a≤6,解得a≤2,又a≥1, ∴1≤a≤2; 综上所述,-2≤a≤2.
【解析】(1)设F(x)=f(x)﹣g(x).①若a= ![]() ,由F(x)=0,即可求得F(x)的零点;②若函数y=F(x)存在零点,则x﹣a=a|x|,等号两端构造两个函数,当a>0时,在同一坐标系中作出两函数的图象,即可求得满足题意的a的取值范围的一部分;同理可得当a<0时的情况,最后取并即可求得a的取值范围.(2)h(x)=f(x)+g(x),x∈[﹣2,2],对任意x1,x2∈[﹣2,2],|h(x1)﹣h(x2)|≤6恒成立h(x1)max﹣h(x2)min≤6,分a≤﹣1、﹣1<a<1、a≥1三类讨论,即可求得a的取值范围.
,由F(x)=0,即可求得F(x)的零点;②若函数y=F(x)存在零点,则x﹣a=a|x|,等号两端构造两个函数,当a>0时,在同一坐标系中作出两函数的图象,即可求得满足题意的a的取值范围的一部分;同理可得当a<0时的情况,最后取并即可求得a的取值范围.(2)h(x)=f(x)+g(x),x∈[﹣2,2],对任意x1,x2∈[﹣2,2],|h(x1)﹣h(x2)|≤6恒成立h(x1)max﹣h(x2)min≤6,分a≤﹣1、﹣1<a<1、a≥1三类讨论,即可求得a的取值范围.

【题目】某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程 ![]() =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46
B.40
C.38
D.58