题目内容
【题目】已知等比数列{an}的公比q>1,a1=1,且a1 , a3 , a2+14成等差数列,数列{bn}满足a1b1+a2b2+…+anbn=(n﹣1)3n+1(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)令cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】
(1)解:等比数列{an}的公比q>1,a1=1,且a1,a3,a2+14成等差数列,
∴2q2=1+q+14,解得q=3,
∴an=3n﹣1.
∵数列{bn}满足a1b1+a2b2+…+anbn=(n﹣1)3n+1(n∈N*).
∴n=1时,a1b1=1,解得b1=1.
n≥2时,a1b1+a2b2+…+an﹣1bn﹣1=(n﹣2)3n﹣1+1,
可得:anbn=(2n﹣1)3n﹣1,∴bn=2n﹣1.(n=1时也成立).
∴bn=2n﹣1.
(2)解:cn=(﹣1)n ![]() =(﹣1)n
=(﹣1)n ![]() =(﹣1)n
=(﹣1)n ![]() ,
,
∴n=2k(k∈N*)时,数列{cn}的前n项和Tn=﹣ ![]() +
+ ![]() +…﹣
+…﹣ ![]() +
+ ![]() =
= ![]() =
= ![]() .
.
n=2k﹣1(k∈N*)时,数列{cn}的前n项和Tn=Tn+1﹣cn+1= ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() .
.
∴Tn= 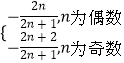 .
.
【解析】(1)利用等差数列与等比数列的通项公式、递推关系即可得出.(2)cn=(﹣1)n ![]() =(﹣1)n
=(﹣1)n ![]() ,对n分类讨论即可得出.
,对n分类讨论即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系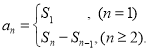 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销 ![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(1)求 ![]() 关于
关于 ![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.