题目内容
7.已知点P(x,y)在椭圆C:2x2+y2=4上,则2x+y的取值范围是$[-2\sqrt{3},2\sqrt{3}]$,椭圆C上的点到M(1,0)的距离的最大值为$\sqrt{6}$.分析 化椭圆方程为标准方程,由动点P(x,y)在椭圆2x2+y2=4上,可设x=2cosθ,y=sinθ,θ∈[0,2π].代入2x+y后化积得答案;利用两点间的距离公式表示出距离|PM|,利用二次函数的性质及余弦函数的值域,即可确定出距离|PM|的最值.
解答 解:由2x2+y2=4,得$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$,
∵动点P(x,y)在椭圆$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$上,
∴可设x=$\sqrt{2}$cosθ,y=2sinθ,θ∈[0,2π].
∴2x+y=2$\sqrt{2}$cosθ+2sinθ=2$\sqrt{3}$sin(θ+φ)(tanφ=$\sqrt{2}$).
∴2x+y∈$[-2\sqrt{3},2\sqrt{3}]$;
$|PM{|}^{2}=(\sqrt{2}cosθ-1)^{2}+(2sinθ)^{2}$=$2co{s}^{2}θ+4si{n}^{2}θ-2\sqrt{2}cosθ+1$
=$3+2(1-co{s}^{2}α)-2\sqrt{2}cosθ$=$-2co{s}^{2}θ-2\sqrt{2}cosθ+5$.
当cosθ=-$\frac{\sqrt{2}}{2}$时,(|PM|2)max=6,
∴椭圆C上的点到M(1,0)的距离的最大值为$\sqrt{6}$.
故答案为:$[-2\sqrt{3},2\sqrt{3}],\sqrt{6}$.
点评 本题考查了椭圆的参数方程、两角和差的正弦公式及其单调性,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
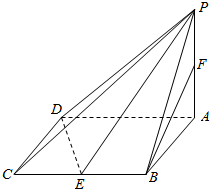 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.