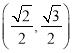题目内容
【题目】有一名同学家开了一个小卖部，他为了研究气温对某种引领销售的影响，记录了2015年7月至12月每月15号下午14时的气温和当天的饮料杯数，得到如下资料：
该同学确定的研究方案是：现从这六组数据中选取2组，用剩下的4组数据取线性回归方程，再用被选中的2组数据进行检验.
（1）求选取2组数据恰好是相邻两个月的概率；
（2）若选中的是8月与12月的两组数据，根据剩下的4组数据，求出
关于
的线性回归方程
；
（3）若有线性回归方程得到估计，数据与所宣称的检验数据的误差不超过3杯，则认为得到的线性回归方程是理想的，请问（2）所得线性回归方程是否理想.
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为： 
， 
， 
.
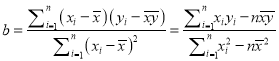【答案】（1）
（2）
（3）见解析
【解析】试题分析：（1）先根据枚举法确定从这六组数据中选取2组的总事件数，再从中挑出满足条件的事件数，最后根据古典概型概率公式求概率（2）先求平均数，再将数据代入公式求
以及
（3）根据所求线性回归方程估计数据，并与实验数据比较，根据差与3大小作出判断
试题解析：（1）从这六组数据中选取2组，共有15种等可能情况，
分别为
，
其中选取2组数据恰好是相邻两个月有5中情况，分别为
，
故求选取2组数据恰好是相邻两个月的概率为
.
（2）
，
关于
的线性回归方程为
.
（3）当
， 
，
当
时， 
， 
，
可以认为得到的线性回归方程是理想的.
练习册系列答案
阅读快车系列答案
相关题目
