题目内容
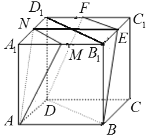
【题目】如图，正方体
中，M，N，E，F分别是棱A1B1，A1D1，B1C1，C1D1的中点，求证：平面AMN∥平面EFDB．
【答案】见解析
【解析】证明：如图所示，连接B1D1，NE，
∵M，N，E，F分别是棱A1B1，A1D1，B1C1，C1D1的中点，
∴MN∥B1D1，EF∥B1D1，∴MN∥EF，
又∵MN面EFDB，EF面EFDB，∴MN∥面EFDB.
∵在正方形A1B1C1D1中，N，E分别是棱A1D1，B1C1的中点，
∴NE∥A1B1且NE=A1B1，又∵A1B1∥AB且A1B1=AB，
∴NE∥AB且NE=AB，∴四边形ABEN是平行四边形.
∴AN∥BE，又∵AN面EFDB，BE面EFDB，∴AN∥面EFDB.
∵AN面AMN，MN面AMN，且AN∩MN=N，
∴平面AMN∥平面EFDB.
练习册系列答案
相关题目
【题目】一个年级有12个班,每个班有50名学生,按1到50排学号,为了交流学习经验,要求每班学号为14的学生留下进行交流,这里运用的是( )
A. 分层抽样 B. 抽签法
C. 随机数表法 D. 系统抽样
