题目内容
【题目】在直角坐标平面内,已知![]() ,其中
,其中![]() 为正整数,对于平面上任意一点
为正整数,对于平面上任意一点![]() ,记
,记![]() 为
为![]() 关于
关于![]() 的对称点,
的对称点,![]() 为
为![]() 关于
关于![]() 的对称点,…
的对称点,…![]() 为
为![]() 关于
关于![]() 的对称点.
的对称点.
(1)求向量![]() 的坐标;
的坐标;
(2)对于任意偶数![]() ,用
,用![]() 表示向量
表示向量![]() 的坐标;
的坐标;
(3)当点![]() 在函数
在函数![]() 图像上移动时,点
图像上移动时,点![]() 形成的是函数
形成的是函数![]() 的图像,其中
的图像,其中![]() 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当![]() 时,
时,![]() ,求:函数
,求:函数![]() 在
在![]() 上的解析式.
上的解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 时,
时,![]()
【解析】
(1)设![]() ,根据对称得到
,根据对称得到![]() ,
,![]() 得到答案.
得到答案.
(2)根据![]() ,代入数据计算得到答案.
,代入数据计算得到答案.
(3)先根据平移得到![]() 时,
时,![]() ,再判断函数
,再判断函数![]() 是以3为周期的周期函数,代入数据得到答案.
是以3为周期的周期函数,代入数据得到答案.
(1)设![]() ,则
,则![]() 满足:
满足:
![]() 满足:
满足: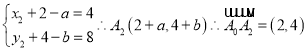
(2)![]()
![]()


(3)![]() 的图像由
的图像由![]() 的图像向右平移
的图像向右平移![]() 个单位,向上平移
个单位,向上平移![]() 个单位得到.
个单位得到.
![]() 是以3为周期的周期函数,故
是以3为周期的周期函数,故![]() 是以3为周期的周期函数
是以3为周期的周期函数
当![]() 时,
时,![]() ,故
,故![]() 时,
时,![]()
故![]() 时,
时,![]()

练习册系列答案
相关题目
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间的零件,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)![]() [22.1,22.2)的记为二等品,尺寸在[21.7,21.8)
[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)![]() [22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
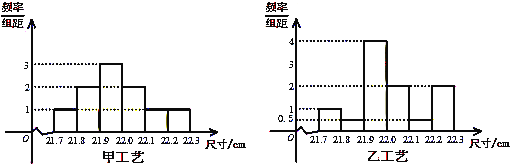
(Ⅰ)根据上述数据完成下列2×2列联表,根据此数据你认为选择不同的工艺与一等品产出率是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
P(K2≥k) | 0.1 | 0.05 | 0.01 |
k | 2.706 | 3.841 | 6.635 |
附:![]() ,其中
,其中![]() .
.
(Ⅱ)以上述两种工艺中各种产品的频率作为相应产品产出的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,从一件产品的平均利润考虑,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.

