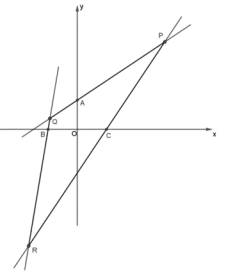
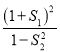题目内容
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
【答案】(1)![]() (2)当
(2)当![]() 时,所需铺草坪面积最小
时,所需铺草坪面积最小
【解析】
(1)建立合适的平面直角坐标系,求出小池塘的边界抛物线方程,然后设出直线![]() 的方程,和抛物线联立,可求出切点坐标, 同时可求出
的方程,和抛物线联立,可求出切点坐标, 同时可求出![]() 的坐标,表示出
的坐标,表示出![]() ,变形即可得结果;
,变形即可得结果;
(2)要所需铺草坪面积最小,需要梯形面积最小,利用(1)的结果表示出梯形面积,利用基本不等式求出最值.
解:(1)以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 作垂直于
作垂直于![]() 轴的直线为
轴的直线为![]() 轴,建立直角坐标系,所以
轴,建立直角坐标系,所以![]() ,
,
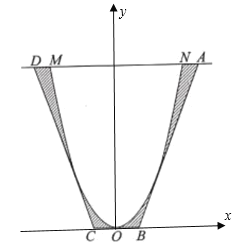
因为小池塘的边界为抛物线型,设边界所在的抛物线方程为![]() ,
,
因为![]() 是曲线上一点,
是曲线上一点,
所以![]() ,即抛物线方程为
,即抛物线方程为![]() .
.
设![]() 所在的直线方程:
所在的直线方程:![]() ,
,
联立![]() ,即
,即![]() ,
,
因为![]() 与抛物线相切,
与抛物线相切,
所以![]() ①.
①.
记直线![]() 与抛物线切于点
与抛物线切于点![]() ,
,
所以![]() 点的横坐标为
点的横坐标为![]() ,即
,即![]() .
.
易得点![]() ,点
,点![]() ,由对称性可知
,由对称性可知![]() ,点
,点![]() .
.
所以小路总长为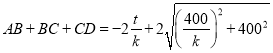 ,
,
由①及![]() 可知
可知
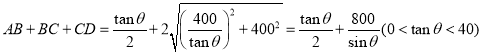 ;
;
(2)记草坪面积为![]() ,梯形面积为
,梯形面积为![]() ,小池塘面积为
,小池塘面积为![]() ,
,
所以![]() ,因为小池塘面积
,因为小池塘面积![]() 为定值,要使得草坪面积最小,则梯形面积最小
为定值,要使得草坪面积最小,则梯形面积最小
![]() ,
,
由①知![]() ,当且仅当“
,当且仅当“![]() ”取得“=”
”取得“=”
所以当![]() 时,梯形面积最小,即草坪面积最小.
时,梯形面积最小,即草坪面积最小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目