题目内容
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
【答案】(1)![]() .(2)见解析。
.(2)见解析。
【解析】试题分析:(1)根据![]() ,
, ![]() 两点关于y轴对称,由椭圆的对称性可知C经过
两点关于y轴对称,由椭圆的对称性可知C经过![]() ,
, ![]() 两点.另外由
两点.另外由![]() 知,C不经过点P1,所以点P2在C上.因此
知,C不经过点P1,所以点P2在C上.因此![]() 在椭圆上,代入其标准方程,即可求出C的方程;(2)先设直线P2A与直线P2B的斜率分别为k1,k2,再设直线l的方程,当l与x轴垂直时,通过计算,不满足题意,再设l:
在椭圆上,代入其标准方程,即可求出C的方程;(2)先设直线P2A与直线P2B的斜率分别为k1,k2,再设直线l的方程,当l与x轴垂直时,通过计算,不满足题意,再设l: ![]() (
(![]() ),将
),将![]() 代入
代入![]() ,写出判别式,利用根与系数的关系表示出x1+x2,x1x2,进而表示出
,写出判别式,利用根与系数的关系表示出x1+x2,x1x2,进而表示出![]() ,根据
,根据![]() 列出等式表示出
列出等式表示出![]() 和
和![]() 的关系,从而判断出直线恒过定点.
的关系,从而判断出直线恒过定点.
试题解析:(1)由于![]() ,
, ![]() 两点关于y轴对称,故由题设知C经过
两点关于y轴对称,故由题设知C经过![]() ,
, ![]() 两点.
两点.
又由![]() 知,C不经过点P1,所以点P2在C上.
知,C不经过点P1,所以点P2在C上.
因此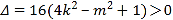 ,解得
,解得![]() .
.
故C的方程为![]() .
.
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知![]() ,且
,且![]() ,可得A,B的坐标分别为(t,
,可得A,B的坐标分别为(t, ![]() ),(t,
),(t, ![]() ).
).
则![]() ,得
,得![]() ,不符合题设.
,不符合题设.
从而可设l: ![]() (
(![]() ).将
).将![]() 代入
代入![]() 得
得
![]()
由题设可知![]() .
.
设A(x1,y1),B(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
而![]()
![]()
![]() .
.
由题设![]() ,故
,故![]() .
.
即![]() .
.
解得![]() .
.
当且仅当![]() 时,
时, ![]() ,欲使l:
,欲使l: ![]() ,即
,即![]() ,
,
所以l过定点(2, ![]() )
)
点睛:椭圆的对称性是椭圆的一个重要性质,判断点是否在椭圆上,可以通过这一方法进行判断;证明直线过定点的关键是设出直线方程,通过一定关系转化,找出两个参数之间的关系式,从而可以判断过定点情况.另外,在设直线方程之前,若题设中未告知,则一定要讨论直线斜率不存在和存在两种情况,其通法是联立方程,求判别式,利用根与系数的关系,再根据题设关系进行化简.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】商丘市大型购物中心——万达广场将于2018年7月6日全面开业,目前正处于试营业阶段,某按摩椅经销商为调查顾客体验按摩椅的时间,随机调查了50名顾客,体验时间(单位:分钟)落在各个小组的频数分布如下表:
体验 时间 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)求这![]() 名顾客体验时间的样本平均数
名顾客体验时间的样本平均数![]() ,中位数
,中位数![]() ,众数
,众数![]() ;
;
(2)已知体验时间为![]() 的顾客中有2名男性,体验时间为
的顾客中有2名男性,体验时间为![]() 的顾客中有3名男性,为进一步了解顾客对按摩椅的评价,现随机从体验时间为
的顾客中有3名男性,为进一步了解顾客对按摩椅的评价,现随机从体验时间为![]() 和
和![]() 的顾客中各抽一人进行采访,求恰抽到一名男性的概率.
的顾客中各抽一人进行采访,求恰抽到一名男性的概率.
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图. 
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附:K2= ![]() .
.