题目内容
11.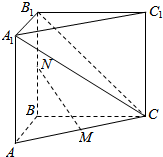 如图在三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,侧面ABB1A1是矩形,M,N分别是AC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,侧面ABB1A1是矩形,M,N分别是AC,BB1的中点.(1)证明:MN∥面A1B1C;
(2)证明:面A1B1C⊥面BCC1B1.
分析 (1)取A1A的中点E,连接NE,ME,证明平面MNE∥面A1B1C,即可证明MN∥面A1B1C;
(2)通过证明在与平面垂直,然后利用平面与平面垂直的判定定理证明即可.
解答  (1)证明:取A1A的中点E,连接NE,ME,则NE∥A1B1,
(1)证明:取A1A的中点E,连接NE,ME,则NE∥A1B1,
∵NE?面A1B1C,A1B1?面A1B1C,
∴NE∥面A1B1C.
∵M是AC的中点,
∴ME∥A1C,
∵ME?面A1B1C,A1C?面A1B1C,
∴ME∥面A1B1C.
∵NE∩ME=E,
∴平面MNE∥面A1B1C.
∵MN?平面MNE,
∴MN∥面A1B1C;
(2)解:∵直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,可得AB⊥BC,
侧面ABB1A1是矩形,可得AB⊥BB1,BC∩BB1=B,
∴AB⊥平面BCC1B1.
∵A1B1∥AB,
∴A1B1⊥平面BCC1B1,∴A1B1?平面A1B1C,
∴面A1B1C⊥面BCC1B1.
点评 本题考查线面、面面平行以及垂直的判定,考查点面距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
19.已知函数f(x)=1+cos$\frac{ωπ}{3}$x,其中ω的值是抛掷一枚均匀的骰子所得的点数,则函数f(x)在区间[0,4]上有5个以下或6个以上(不含5个和6个)函数值为1的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
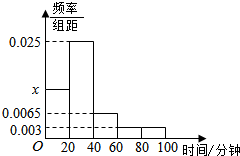 古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].
古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].