题目内容
10.某市有三支广场舞队伍,已知A队有队员60人,B队有队员90人,C队有队员m人,现用分层抽样的方法从这三个广场舞队伍中随机抽取n名队员进行问卷调查,已知从A队中抽取的人数比从B队抽取的人数少1人.(1)求从A队中抽取的人数;
(2)已知m=30,若从参与问卷调查的队员中抽取3人进行回访,求回访的3人来自于A队的人数X的分布列及数学期望.
分析 (1)由已知条件求出抽样比f=$\frac{1}{90-60}$=$\frac{1}{30}$,由此能求出从A队中抽取的人数.
(2)由已知得X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)∵A队有队员60人,B队有队员90人,C队有队员m人,
现用分层抽样的方法从这三个广场舞队伍中随机抽取n名队员进行问卷调查,
从A队中抽取的人数比从B队抽取的人数少1人,
∴抽样比f=$\frac{1}{90-60}$=$\frac{1}{30}$,
∴从A队中抽取的人数为:60×$\frac{1}{30}$=2(人).
(2)当m=30时,由已知得用分层抽样的方法A队抽出2人,B队抽出3人,C队抽出1人进行问卷调查,
从参与问卷调查的队员中抽取3人进行回访,回访的3人来自于A队的人数X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{4}{20}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{{C}_{6}^{3}}$=$\frac{12}{20}$,
P(X=2)=$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{4}{20}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{4}{20}$ | $\frac{12}{20}$ | $\frac{4}{20}$ |
点评 本题考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型,解题时要注意排列组合知识的合理运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
14.斜率k=-$\frac{5}{4}$,且过点A(1,5)的直线l与x轴交于点P,则点P的坐标为( )
| A. | (3.4,0) | B. | (13,0) | C. | (5,0) | D. | (1,0) |
15.已知随机变量ξ的数学期望为E(ξ),方差为D(ξ),随机变量η=$\frac{ξ-Eξ}{\sqrt{Dξ}}$,则D(η)的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | $\sqrt{D(ξ)}$ |
19.已知函数f(x)=1+cos$\frac{ωπ}{3}$x,其中ω的值是抛掷一枚均匀的骰子所得的点数,则函数f(x)在区间[0,4]上有5个以下或6个以上(不含5个和6个)函数值为1的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
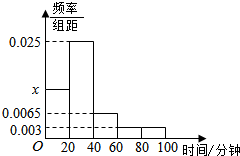 古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].
古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].