题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
=0相切.
(Ⅰ)求椭圆C的方程;
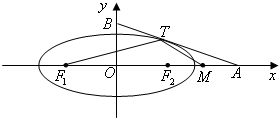
(Ⅱ)设P(4,0),M,N是椭圆C上关于x轴对称的任意两个不同的点,连接PN交椭圆C于另一点E,求直线PN的斜率的取值范围;
(Ⅲ)在(Ⅱ)的条件下,证明直线ME与x轴相交于定点.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P(4,0),M,N是椭圆C上关于x轴对称的任意两个不同的点,连接PN交椭圆C于另一点E,求直线PN的斜率的取值范围;
(Ⅲ)在(Ⅱ)的条件下,证明直线ME与x轴相交于定点.
(Ⅰ)由题意知e=
=
,
所以e2=
=
=
,即a2=4b2,∴a=2b
又因为b=
=1,∴a=2,故椭圆C的方程为C:
+y2=1.(4分)
(Ⅱ)由题意知直线PN的斜率存在,设直线PN的方程为y=k(x-4).
由
得(4k2+1)x2-32k2x+64k2-4=0.①(6分)
由△=(-32k2)2-4(4k2+1)(64k2-4)>0,得12k2-1<0,∴-
<k<
(8分)
又k=0不合题意,所以直线PN的斜率的取值范围是:(-
,0)∪(0,
).(9分)
(Ⅲ)设点N(x1,y1),E(x2,y2),则M(x1,-y1).
直线ME的方程为y-y2=
(x-x2).令y=0,得x=x2-
.(11分)
将y1=k(x1-4),y2=k(x2-4)代入整理,得x=
.②
由①得x1+x2=
,x1x2=
代入②整理,得x=1.(13分)
所以直线ME与x轴相交于定点(1,0).(14分)
| c |
| a |
| ||
| 2 |
所以e2=
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
又因为b=
| ||
|
| x2 |
| 4 |
(Ⅱ)由题意知直线PN的斜率存在,设直线PN的方程为y=k(x-4).
由
|
由△=(-32k2)2-4(4k2+1)(64k2-4)>0,得12k2-1<0,∴-
| ||
| 6 |
| ||
| 6 |
又k=0不合题意,所以直线PN的斜率的取值范围是:(-
| ||
| 6 |
| ||
| 6 |
(Ⅲ)设点N(x1,y1),E(x2,y2),则M(x1,-y1).
直线ME的方程为y-y2=
| y2+y1 |
| x2-x1 |
| y2(x2-x1) |
| y2+y1 |
将y1=k(x1-4),y2=k(x2-4)代入整理,得x=
| 2x1x2-4(x1+x2) |
| x1+x2-8 |
由①得x1+x2=
| 32k2 |
| 4k2+1 |
| 64k2-4 |
| 4k2+1 |
所以直线ME与x轴相交于定点(1,0).(14分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目