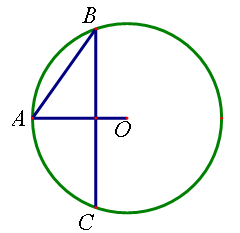
题目内容
如图,已知椭圆C:
+
=1(a>b>0)的离心率为
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
(1)求椭圆C的方程;
(2)求
•
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR|•|OS|为定值.

| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)求
| TM |
| TN |
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR|•|OS|为定值.

(1)依题意,得a=2,e=
=
,
∴c=
,b=
=1,
故椭圆C的方程为
+y2=1.…(3分)
(2)方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,所以y12=1-
.(*)…(4分)
由已知T(-2,0),则
=(x1+2,y1),
=(x1+2,-y1),
∴
•
=(x1+2,y1)•(x1+2,-y1)
=(x1+2)2-y12
=(x1+2)2-(1-
)=
x12+4x1+3
=
(x1+
)2-
.…(6分)
由于-2<x1<2,
故当x1=-
时,
•
取得最小值为-
.
由(*)式,y1=
,故M(-
,
),
又点M在圆T上,代入圆的方程得到r2=
.
故圆T的方程为:(x+2)2+y2=
.…(8分)
方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,由已知T(-2,0),
则
•
=(2cosθ+2,sinθ)•(2cosθ+2,-sinθ)
=(2cosθ+2)2-sin2θ
=5cos2θ+8cosθ+3
=5(cosθ+
)2-
.…(6分)
故当cosθ=-
时,
•
取得最小值为-
,
此时M(-
,
),
又点M在圆T上,代入圆的方程得到r2=
.
故圆T的方程为:(x+2)2+y2=
.…(8分)
(3)方法一:设P(x0,y0),
则直线MP的方程为:y-y0=
(x-x0),
令y=0,得xR=
,
同理:xS=
,…(10分)
故xR•xS=
(**)…(11分)
又点M与点P在椭圆上,
故x02=4(1-y02),x12=4(1-y12),…(12分)
代入(**)式,
得:xR•xS=
=
=4.
所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.…(14分)
方法二:设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为:y-sinα=
(x-2cosα),
令y=0,得xR=
,
同理:xS=
,…(12分)
故xR•xS=
=
=4.
所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.…(14分)
| c |
| a |
| ||
| 2 |
∴c=
| 3 |
| 4-3 |
故椭圆C的方程为
| x2 |
| 4 |
(2)方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,所以y12=1-
| x12 |
| 4 |
由已知T(-2,0),则
| TM |
| TN |
∴
| TM |
| TN |
=(x1+2)2-y12
=(x1+2)2-(1-
| x12 |
| 4 |
| 5 |
| 4 |
=
| 5 |
| 4 |
| 8 |
| 5 |
| 1 |
| 5 |
由于-2<x1<2,
故当x1=-
| 8 |
| 5 |
| TM |
| TN |
| 1 |
| 5 |
由(*)式,y1=
| 3 |
| 5 |
| 8 |
| 5 |
| 3 |
| 5 |
又点M在圆T上,代入圆的方程得到r2=
| 13 |
| 25 |
故圆T的方程为:(x+2)2+y2=
| 13 |
| 25 |
方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,由已知T(-2,0),
则
| TM |
| TN |
=(2cosθ+2)2-sin2θ
=5cos2θ+8cosθ+3
=5(cosθ+
| 4 |
| 5 |
| 1 |
| 5 |
故当cosθ=-
| 4 |
| 5 |
| TM |
| TN |
| 1 |
| 5 |
此时M(-
| 8 |
| 5 |
| 3 |
| 5 |
又点M在圆T上,代入圆的方程得到r2=
| 13 |
| 25 |
故圆T的方程为:(x+2)2+y2=
| 13 |
| 25 |
(3)方法一:设P(x0,y0),
则直线MP的方程为:y-y0=
| y0-y1 |
| x0-x1 |
令y=0,得xR=
| x1y0-x0y1 |
| y0-y1 |
同理:xS=
| x1y0+x0y1 |
| y0+y1 |
故xR•xS=
| x12y02-x02y12 |
| y02-y12 |
又点M与点P在椭圆上,
故x02=4(1-y02),x12=4(1-y12),…(12分)
代入(**)式,
得:xR•xS=
| 4(1-y12)y02-4(1-y02)y12 |
| y02-y12 |
| 4(y02-y12) |
| y02-y12 |
所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.…(14分)
方法二:设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为:y-sinα=
| sinα-sinθ |
| 2cosα-2cosθ |
令y=0,得xR=
| 2(sinαcosθ-cosαsinθ) |
| sinα-sinθ |
同理:xS=
| 2(sinαcosθ+cosαsinθ) |
| sinα+sinθ |
故xR•xS=
| 4(sin2αcos2θ-cos2αsin2θ) |
| sin2α-sin2θ |
| 4(sin2α-sin2θ) |
| sin2α-sin2θ |
所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.…(14分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
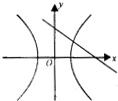



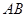 ,
,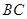 是
是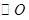 的两条弦,
的两条弦, ,
,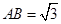 ,
,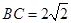 ,则
,则