��Ŀ����
12��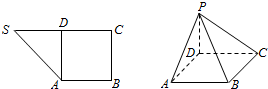 ��ͼ1����ֱ������SABC�У���B=��C=$\frac{��}{2}$��DΪ��SC�ϵĵ㣬��AD��SC���ֽ���SAD��AD����PAD��λ�ã�������S��ΪP������ʹ��PA��AB��
��ͼ1����ֱ������SABC�У���B=��C=$\frac{��}{2}$��DΪ��SC�ϵĵ㣬��AD��SC���ֽ���SAD��AD����PAD��λ�ã�������S��ΪP������ʹ��PA��AB����1����֤��PD��ƽ��ABCD��
��2����֪PD=AD��PD+AD+DC=6�����߶�PBȡ����Сֵʱ�������������⣺
�����E����$\overrightarrow{BE}$=��$\overrightarrow{BP}$��0�ܦˡ�1�������Ƿ���ڦˣ�ʹ��ƽ��EAC��ƽ��PDC���ɵ������$\frac{��}{3}$�������ڣ�����ˣ��������ڣ���˵�����ɣ�
����G��AD���е㣬����ƽ��PBC���Ƿ���ڵ�F��ʹ��FG��ƽ��PBC�������ڣ�ȷ����F��λ�ã��������ڣ���˵�����ɣ�
���� ��1���������洹ֱ���ж���������֤��PD��ƽ��ABCD��
��2�������ռ�����ϵ�����ƽ��ķ�����������������������⼴�ɣ�
���  ֤������1����PA��AB��AB��AD��PA��AD=A��
֤������1����PA��AB��AB��AD��PA��AD=A��
��AB��ƽ��PAD��
��PD?ƽ��PAD��
��AB��PD��
��PD��AD��AD��AB=A��
��PD��ƽ��ABCD
��2����PD=x����AD=x��DC=6-2x��
��PB2=x2+x2+��6-2x��2=6��x-2��2+12�����ҽ���x=2ʱ��PB2ȡ����Сֵ��
��PBȡ����Сֵ��
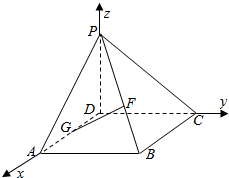
����DΪԭ�㣬DA��DC��DP�ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵD-xyz��
��PD=AD=2��
��A��2��0��0����B��2��2��0����C��0��2��0����P��0��0��2����
$\overrightarrow{CB}$=��2��0��0����$\overrightarrow{BP}$=��-2��-2��2����
$\overrightarrow{CA}$=��2��-2��0����
�ٴ��ڣ���ʵ�ϣ�$\overrightarrow{CE}=\overrightarrow{CB}+\overrightarrow{BE}$=$\overrightarrow{CB}+��\overrightarrow{BP}$=��2-2�ˣ�-2�ˣ�2�ˣ���
��$\overrightarrow{n}$=��x��y��z����ƽ��ACE��һ����������
��$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CE}=0}\\{\overrightarrow{n}•\overrightarrow{CA}=0}\end{array}\right.$����$\left\{\begin{array}{l}{��2-2�ˣ�x-2��y+2��z=0}\\{2x-2y=0}\end{array}\right.$��
ȡ$\overrightarrow{n}$=���ˣ��ˣ�2��-1����
��$\overrightarrow{m}$=��1��0��0����ƽ��PCD��һ����������
��cos$\frac{��}{3}$=|cos��$\overrightarrow{m}��\overrightarrow{n}$��|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=$\frac{|��|}{\sqrt{2{��}^{2}+��2��-1��^{2}}}$=$\frac{1}{2}$��
��00���ˣ�1�����=1-$\frac{\sqrt{2}}{2}$��
������ڵ�F�������⣬����F��ƽ��PBC�ϣ����Ǵ���m��nʹ$\overrightarrow{CF}=m\overrightarrow{CB}+n\overrightarrow{CP}$��
$\overrightarrow{GF}=\overrightarrow{GC}+\overrightarrow{CF}=\overrightarrow{GC}$$+m\overrightarrow{CB}+n\overrightarrow{CP}$=��-1+2m��2-2n��2n����
ע�����ֱ��������PDC��б���ϵ�ֱ�ߴ�ֱ��ƽ��PBC��
��$\overrightarrow{{n}_{1}}$=��0��0��1����ƽ��PBC��һ����������
��$\overrightarrow{{n}_{1}}$��$\overrightarrow{CF}$����$\left\{\begin{array}{l}{-1+2m=0}\\{2-2n=2n}\end{array}\right.$��
���m=n=$\frac{1}{2}$����ʱ��F��1��1��1������
����ƽ��PBC���Ǵ���PB���е�F��ʹ��FG��ƽ��PBC��
���� ������Ҫ���������洹ֱ�Ķ�����ж�������Ӧ�ã�ƽ�����������㣬�������Ķ����֪ʶ��������ѧ���Ի���֪ʶ���ۺ����ã�

 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
��2����ֱ֪��l��x=my+1����ԲC2�ཻ�ڲ�ͬ����M��N��������$\overrightarrow{OM}��\overrightarrow{ON}$�������m��ֵ��
| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
 ��ͼ��������ABC-A1B1C1�IJ��ⴹֱ�ڵ��棬����߳��Ͳ��ⳤ��Ϊ2��D��BC���е㣮
��ͼ��������ABC-A1B1C1�IJ��ⴹֱ�ڵ��棬����߳��Ͳ��ⳤ��Ϊ2��D��BC���е㣮