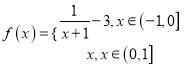题目内容
【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
【答案】(1) U(A∩B)={x|x<2或x≥3}(2) a>-4.
【解析】试题分析:(1)求出集合B中不等式的解集确定出集合B,求出集合A与集合B的公共解集即为两集合的交集,根据全集为R,求出交集的补集即可;
(2)求出集合C中的不等式的解集,确定出集合C,由B与C的并集为集合C,得到集合B为集合C的子集,即集合B包含于集合C,从而列出关于a的不等式,求出不等式的解集即可得到a的范围.
解:(1)由集合B中的不等式2x﹣4≥x﹣2,解得x≥2,
∴B={x|x≥2},又A={x|﹣1≤x<3},
∴A∩B={x|2≤x<3},又全集U=R,
∴U(A∩B)={x|x<2或x≥3};
(2)由集合C中的不等式2x+a>0,解得x>﹣![]() ,
,
∴C={x|x>﹣![]() },
},
∵B∪C=C,
∴BC,
∴﹣![]() <2,解得a>﹣4;
<2,解得a>﹣4;
故a的取值范围为(﹣4,+∞).

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
优 秀 | 不优秀 | |
甲 班 | 10 | 35 |
乙 班 | 7 | 38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
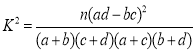
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |