题目内容
如图,四棱锥 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.

(1)求证:平面 平面
平面 ;
;
(2)当 ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出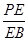 的值.
的值.
 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.
(1)求证:平面
 平面
平面 ;
;(2)当
 ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出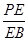 的值.
的值.(1)详见解析;(2) 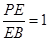 ;(3)
;(3)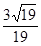 .
.
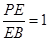 ;(3)
;(3)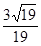 .
.试题分析:(1)证面面垂直,先证明线面垂直.那么证哪条线垂直哪个面?因为ABCD是正方形,
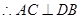 .又由
.又由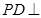 平面
平面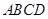 可得
可得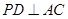 ,所以可证
,所以可证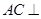 平面
平面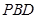 ,从而使问题得证.
,从而使问题得证.(2)设AC交BD=O.由(1)可得
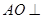 平面
平面 ,所以
,所以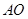 即为三棱锥的高.由条件易得
即为三棱锥的高.由条件易得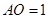 .
.因为
 ,所以可求出底面
,所以可求出底面 的面积.又因为PD=2,所以可求出点E到边PD的距离,从而可确定点E的位置.
的面积.又因为PD=2,所以可求出点E到边PD的距离,从而可确定点E的位置. 试题解析:(1)证明:
 四边形ABCD是正方形ABCD,
四边形ABCD是正方形ABCD,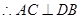 .
. 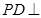 平面
平面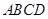 ,
, 平面
平面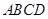 ,所以
,所以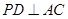 .
. ,所以
,所以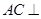 平面
平面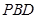 .
.因为
 平面
平面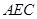 ,所以平面
,所以平面 平面
平面 .
.(2) 设
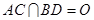 .
.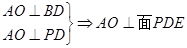 ,
,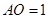 .
.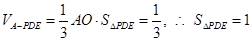
在直角三角形ADB中,DB=PD=2,则PB=
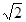
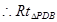 中斜边PB的高h=
中斜边PB的高h=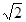
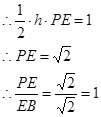
即E为PB的中点.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 中,AC⊥BC,AB⊥
中,AC⊥BC,AB⊥ ,
, ,D为AB的中点,且CD⊥
,D为AB的中点,且CD⊥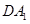 。
。
 ⊥平面ABC;
⊥平面ABC; 的体积。
的体积。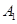 点出发沿正方体的表面到达点
点出发沿正方体的表面到达点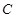 的最短路程为 .
的最短路程为 .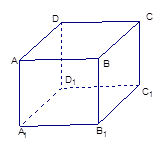
 ,那么这个三棱锥的体积是 .
,那么这个三棱锥的体积是 . 的正方体
的正方体 中, P、Q是对角线
中, P、Q是对角线 上的点,若
上的点,若 ,则三棱锥
,则三棱锥 的体积为 ( )
的体积为 ( )


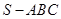 中,
中,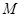 、
、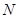 分别是
分别是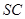 、
、 的中点,且
的中点,且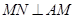 ,若侧棱
,若侧棱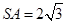 ,则正三棱锥
,则正三棱锥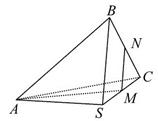








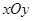 平面上,将两个半圆弧
平面上,将两个半圆弧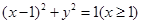 和
和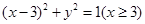 、两条直线
、两条直线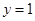 和
和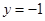 围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为
围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为 ,过
,过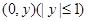 作
作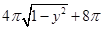 ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理、一个平放的圆柱和一个长方体,得出