题目内容
已知函数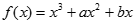 在
在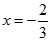 与
与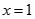 处都取得极值.
处都取得极值.
(1)求函数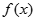 的解析式;
的解析式;
(2)求函数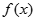 在区间[-2,2]的最大值与最小值.
在区间[-2,2]的最大值与最小值.
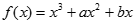 在
在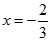 与
与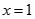 处都取得极值.
处都取得极值.(1)求函数
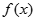 的解析式;
的解析式;(2)求函数
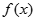 在区间[-2,2]的最大值与最小值.
在区间[-2,2]的最大值与最小值.(1)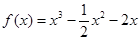 ;(2)
;(2)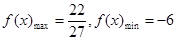 .
.
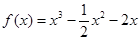 ;(2)
;(2)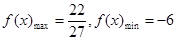 .
.试题分析:(1)由已知函数
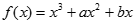 在
在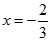 与
与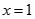 处都取得极值,得到
处都取得极值,得到 ,求出
,求出 得到:关于a,b的两个方程,联立解方程组可得到a,b的值,从而可写出函数
得到:关于a,b的两个方程,联立解方程组可得到a,b的值,从而可写出函数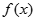 的解析式;(2)由(1)已求出
的解析式;(2)由(1)已求出 的解析式,要求函数
的解析式,要求函数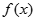 在区间[-2,2]的最大值与最小值,只需先求出函数
在区间[-2,2]的最大值与最小值,只需先求出函数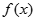 在区间[-2,2]的极大值与极小值,再求出两个端点的函数值,然后比较这四个数值的大小,得其中的最大者就是该函数的最大值,最小者就是该函数的最小值.
在区间[-2,2]的极大值与极小值,再求出两个端点的函数值,然后比较这四个数值的大小,得其中的最大者就是该函数的最大值,最小者就是该函数的最小值.试题解析:(1)f(x)=x3+ax2+bx,f¢(x)=3x2+2ax+b 1分
由f¢(
 )=
)= ,f¢(1)=3+2a+b=0 3分
,f¢(1)=3+2a+b=0 3分得a=
 ,b=-2 5分
,b=-2 5分经检验,a=
 ,b=-2符合题意
,b=-2符合题意所以,所求的函数解析式为:
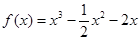 6分
6分 (2)由(1)得f¢(x)=3x2-x-2=(3x+2)(x-1), 7分
列表如下:
| x | (-2,-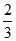 ) ) | -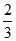 | (-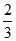 ,1) ,1) | 1 | (1,2) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 | ¯ | 极小值 | |
 11分
11分 所以当
 时,
时, 12分
12分
练习册系列答案
相关题目
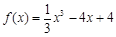 .
.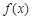 的极值;
的极值;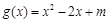 ,对
,对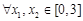 ,都有
,都有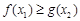 ,求实数m的取值范围.
,求实数m的取值范围. (不含锥形盖内空间),盖子的母线与底面圆半径的夹角为
(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为 ,设粮囤的底面圆半径为R
,设粮囤的底面圆半径为R ,需用白铁皮的面积记为
,需用白铁皮的面积记为 (不计接头等)。
(不计接头等)。 表示为R的函数;
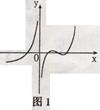
表示为R的函数;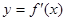 的图象可能为( )
的图象可能为( )
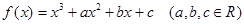 ,若函数
,若函数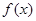 在区间
在区间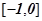 上是单调减函数,则
上是单调减函数,则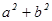 的最小值为
的最小值为
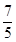


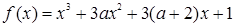 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数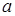 的取值范围是 。
的取值范围是 。 的图象经过原点,
的图象经过原点, 若
若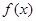 在
在 取得极大值2。
取得极大值2。 的解析式;
的解析式; ,求
,求 的最大值。
的最大值。