题目内容
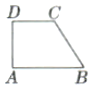
【题目】如图，四边形ABCD为直角梯形，试作出绕其各条边所在的直线旋转所得到的几何体.
【答案】见解析
【解析】
确定旋转直线，根据其余各边与旋转直线的关系，结合圆柱、圆锥、圆台定义，即可求出结论.
以边AD所在直线为轴旋转，形成的几何体是一个圆台，
如图（1）所示.
以边AB所在直线为轴旋转，形成的几何体可以看作是由
一个圆锥和一个圆柱拼接而成的组合体，如图（2）所示.
以边CD所在直线为轴旋转，形成的几何体可以看作是由
一个圆柱挖去一个同底圆锥而成的组合体，如图（3）所示.
以边BC所在直线为轴旋转，形成的几何体可以看作是由
一个圆台挖去一个同底（上底面）圆锥后再和一个同底（下底面）
圆锥拼接而成的组合体，如图（4）所示.
（1） （2） （3） （4）
练习册系列答案
相关题目
【题目】工厂车间某部门有8个小组，在一次技能考试中成绩情况分析如下：
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
大于90分人数 | 6 | 6 | 7 | 3 | 5 | 3 | 3 | 7 |
不大于90分人数 | 39 | 39 | 38 | 42 | 40 | 42 | 42 | 38 |
（1）求90分以上人数
对小组序号
的线性回归方程；
附：回归方程为
，其中
，
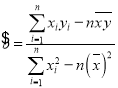．本题
，
.
（2）能否在犯错误的概率不超过0.01的前提下认为7组与8组的成绩是否优秀（大于90分）与小组有关系．附部分临界值表：
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
.
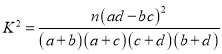